Partial multipliers: when more is less

Ismo Rama and Patrick Lawrence[1]

Economics and Policy Research Branch, Policy and Strategy Group, Victorian Department of Primary Industries

Views expressed in this note are those of the authors and not necessarily those of the Department of Primary Industries or the Victorian Government.

1. Introduction

Investments are often promoted on the grounds that they will generate, or have generated, substantial ‘multiplier’ benefits for the local or regional economy. These multipliers are typically ‘partial’ in the sense that they focus on a particular geographic area or sector of the economy.[2]

Partial multipliers can be distinguished from macroeconomic multipliers that estimate additional shifts in aggregate demand across the wider economy resulting from expansionary fiscal policy, and also from money multipliers that estimate the amount of money the banking system generates with each dollar of reserves (for discussion of each see Stonecash et al, 2003).

This note provides a brief discussion of partial multipliers. The discussion has particular reference to partial multipliers in a public policy context where they are often used to estimate economic impacts flowing from potential government investment or other intervention to support or facilitate new investments in the economy. First we briefly describe partial multipliers, their underlying logic and their calculation, in section 2. Section 3 then discusses important limitations applying to partial multipliers. Section 4 presents an alternative way forward, and section 5 concludes.

We conclude that partial multipliers are subject to a number of important conceptual limitations. From an economic perspective they fail to consider the importance of opportunity cost, may be subject to double - and triple - counting, and do not distinguish between average and marginal impacts. From a financial perspective they do not take account of the presence of negative multipliers due to financing requirements. Further, partial multipliers are subject to data limitations.

As a result partial multipliers offer little practical guidance for public policy. Further, they do not eliminate the need for rigorous analysis of the implications of potential government intervention on the basis of market failure and identification of a role for government, and robust assessment of direct benefits and costs.

2. Partial multipliers - an overview

Partial multipliers are often used by project proponents and policy analysts to estimate the economic impact of a change in a sector or area of the economy. This economic impact can be measured as added employment, output, value added, income or investment. Partial multipliers can be expressed as a ratio (e.g. 2:1), or simply as a number (e.g. 2) – in each case the multiplier indicates that the final impact of (say) an initial investment of $100 will result in $200 of economic activity. The discussion below presents some examples of multipliers, examines the logic of multipliers, and discusses their calculation.

2.1 Examples and uses

Some examples[3] of partial multipliers being applied in Victorian and Australian contexts include the following:

The Minerals Council of Australia suggests that the current employment multiplier for the mining industry in Victoria is 2 (Minerals Council of Australia, 2008). That is, for every job directly employed in Victoria in the mining industry, a total of 2 people (1 additional person) are employed as a result of the secondary economic effects of mining in Victoria.
A 2006 report for the Australian Department of Environment and Heritage suggests: “There are many examples where each dollar invested in regional natural resource management by Australian and State and Territory Governments is leveraging significant returns, conservatively estimated at another $4 for every $1 invested” (Green, 2006). That is, the investment multiplier for government investment in NRM is estimated to be 5.
The Australian Government Minister for Infrastructure, Transport, Regional Development and Local Government recently noted “The Townsville Port Access Road… (had) a significant multiplier effect on the economy” (Albanese, 2008).
The Victorian Government provides support to major events (in areas including sport, culture and fashion) on grounds including the presence of estimated multiplier benefits.[4]

2.2. Logic

The underlying logic of a partial multiplier is that an expansion of economic activity triggered by (perhaps) a new investment in one sector of the economy causes other sectors to expand as well, in a way that would not have happened without the investment. Therefore the total economic impact will be the sum of expansion in both the initial sector and subsequently in the other sectors. (Coughlin and Mandelbaum 1991; Madden 2001). Figure 1 below illustrates the logic behind the calculation of a partial multiplier, using output as the unit of measure.

Figure 1 - The partial multiplier process

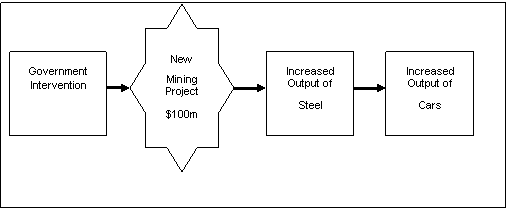
In this stylised example, Government intervention leads to investment in a new mining project, which in-turn increases the value of output in the mining industry by (say) $100 million. This in-turn produces claimed secondary benefits as the output of the mining project moves through the output chain, namely an increased output of steel, and in-turn, cars.

In a public policy context, multipliers are often used to support possible government intervention by attempting to measure the economic impact of a project relative to a base-case of no government intervention (and hence no project).

2.3 Calculation

Partial multipliers have been calculated in different ways ranging from ‘back of the envelope’ measures to more formal approaches.[5] It is beyond the scope of this paper to discuss alternative methodologies in detail, however the more sophisticated approaches include calculation from statistical tables known as input-output tables. These tables provide data about the goods and services produced in each sector and economy (whether it is a country, state or region) and how the benefits and costs from production were spent on other goods and services inside and outside the economy. Input-output tables allow changes in one sector of the economy to be traced through to reveal how they may affect markets in other sectors.[6]

3. Critical analysis

Partial multipliers are subject to conceptual difficulties arising from both economic and financial perspectives.[7] In addition, they are subject to important data constraints. These are discussed below.

3.1 Conceptual limitations - economic

The key conceptual limitations include a failure to consider the importance of opportunity cost, the risk of double – and triple – counting, and a failure to distinguish between average and marginal changes.

Opportunity cost

The main limitation of partial multipliers is that when estimating secondary benefits they do not take into consideration the opportunity cost of using resources that were previously being used elsewhere in the economy, or would have likely been used elsewhere in the economy (Banks, 2002; VAGO, 2002).

Taking the example in figure 1, the increase in the value of output of both steel and cars draws on the increased output of ore (valued at $100 million), and other factors of production (e.g. labour, capital). However, if these other factors of production are drawn from other productive uses in the economy, the value of output elsewhere will be reduced. This will in turn reduce, even fully offset, any claimed multiplier benefits.[8] In other words, multipliers represent genuine gains to the economy only to the extent that the flow-on activities draw on resources that would otherwise not be used, or if they involve more efficient use of those resources (VAGO, 2002).

This issue is clearly illustrated in cases where a partial multiplier claims to estimate the number of jobs to be ‘created’ from an investment. In areas or periods where unemployment is low a new project will not be able to draw labour from a pool of unemployed. In these cases projects will likely ‘divert’ jobs from alternative employment rather than ‘create’ jobs (Henry, 2007). Further, even if unemployed labour is available, if the jobs flowing from the new investment project require specialised skills these may not be readily available among the unemployed. In effect, such claims about job ‘creation’ rely on an implicit assumption that the unemployed would otherwise be permanently unemployed. Capital resources can be similarly diverted from alternative uses in other parts of the economy.

Generally, in competitive markets where resources are fully employed, claimed secondary benefits will not be real. In non-competitive markets, where unemployed resources are present, some secondary benefits may be present (Sinden and Thampapillai, 1995). However even in these circumstances, the project in question would need to draw otherwise permanently unemployed resources (land, labour and capital) directly from these markets.[9]

Supply constraints may also have important economy-wide implications that limit the usefulness of partial multipliers. For example, if unemployment is low and a new investment project results in an increased demand for labour, this may lead to more widespread increases in wages. Increased wages may, in turn, have a negative impact on other sectors of the economy. Partial multipliers ignore such effects, and thus provide an inaccurate estimate of the impact of an investment on the economy.

Double and triple counting

Claimed multiplier benefits may be subject to double-counting and triple-counting, as an initial increase in output[10] flows through the output-chain and is subsequently re-counted in the estimation of multipliers. This is illustrated in figure 2 below.

Figure 2 – Partial multipliers and triple counting

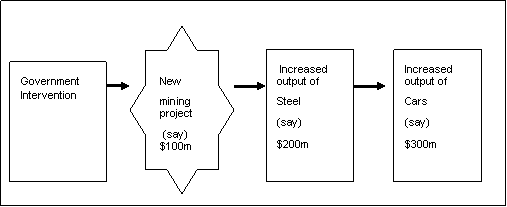
The value of increased output from our hypothetical mining project is $100 million and produces claimed secondary benefits including increased output in the steel industry of $200 million, and increased output in the car industry of $300 million. The claimed secondary benefits are sometimes mistakenly estimated to be ($100 million + $200 million + $300 million), summing to $600 million. The multiplier could now be estimated as 6. However, the increased value of output of the mining project of $100 million is included in the valuation of the mining project itself, and also the steel and car output, and is therefore counted three times.[11] Once this triple-counting has been corrected,[12] the remaining claimed secondary benefits are subject to questions concerning opportunity cost as discussed earlier.

Average and marginal impacts

Partial multipliers that are derived from historical data present relationships between economic variables on average. For example, if historically 100 direct jobs were associated with a genuinely additional[13] 50 indirect jobs, then the jobs-multiplier would be 1.5. However, this is not necessarily an accurate estimate of marginal changes. If a further 100 direct farming jobs were created by a new investment, for example, how many additional indirect jobs (e.g. fruit pickers) would be created? As additional labour becomes more scarce and increasingly costly, it may be that at the margin firms buy capital (e.g. picking machines) rather than employ additional fruit pickers, and so the number of additional indirect jobs flowing from the project declines.[14]

3.2 Conceptual limitations arising from project financing

All projects, whether privately or publicly funded, need to be financed. Privately funded projects are financed through either debt or equity, and government investments are financed either by increasing current taxes, increasing future taxes (a budget deficit), or through reductions in government spending elsewhere. While the new investment may have a positive multiplier effect, the financing requirement will cause a negative multiplier effect. This is illustrated in figure 3 for a hypothetical mining investment with an associated financing requirement. The net multiplier effect associated with this financing requirement will depend on the relative size of both positive and negative multipliers, and may indeed be negative (Madden, 2001).

Figure 3 - Positive and negative multipliers

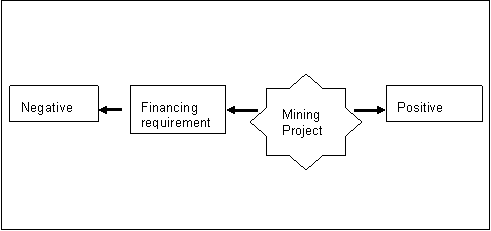
An analysis that ignores this negative multiplier effect will not provide an accurate estimate of the impact of a proposed investment.[15]

3.3 Data constraints

Input-output tables in Australia are produced by the Australian Bureau of Statistics at roughly three-year intervals - the most recent set of tables is for 2004-05 and was released in November 2008 (ABS, 2008). Where input-output relationships change over time, any partial multipliers derived from this data will be unlikely to provide an accurate picture of likely impacts in later years. In some industries input-output relationships may remain relatively stable over time, however other industries may experience more rapid change (Coughlin and Mandelbaum, 1991). Possible reasons for such changes in input-output relationships include:

Changes in climatic conditions can affect input-output relationships, particularly in agricultural industries, and such changes may be significant from one year to the next.
Technological change can influence input patterns – for example some manufacturing industries likely use less steel and more plastic than in the past. Some technological changes may take place over long time frames, however others may subject to sudden shocks and innovation.
Changes in relative prices may also influence input-output relationships, for example increases in oil prices may lead to substitution toward alternative sources of energy.
Policy reform may also change such relationships, for example policy induced increases in water prices have likely changed input-output relationships in the dairy sector in Victoria as farmers have found ways to increase the amount of milk produced for a given amount of water.
Finally, as firms change and adjust over time they may be able to exploit economies of scale that results in changes to input-output relationships.

As a result of such data constraints, partial multipliers derived from such data should be used with caution.

4. A way forward

As a result of these limitations, partial multipliers offer little guidance for public policy. The useful of multipliers is limited to occasions where secondary benefits have no (or little) associated opportunity cost, where double and triple counting has been avoided, where average and marginal impacts are distinguished, where negative multipliers associated with the raising of tax revenue have been considered, and where data is timely and accurate. These circumstances are likely to be relatively rare.

When considering whether, and how, government might facilitate or support investment projects in the economy, a more robust approach is to examine whether projects are subject to market failure, and to consider where there may be a role for government. If market failure is present, attention can then focus on whether government intervention can correct any such failure in a cost effective way – in other words will the benefits of intervention exceed the costs. This analysis of costs and benefits should generally not take into account second round effects (multipliers) for the reasons discussed above. Where these conditions are met (market failure is present, and where the benefits of intervention exceed the costs), community welfare can be enhanced through well designed government intervention regardless of the presence or magnitude of multipliers.

The importance of market failure and cost benefit analysis can be highlighted by the counter-factual. If no market failure is present, and a potential project will generate an appropriate direct return on an investment, investors will face incentives to fund such projects regardless of the presence or size of any partial multiplier. If government invests in such a project on the grounds of a ‘high’ multiplier, it will simply ‘crowd out’ private sector investment that would have taken place anyway. In such circumstances the multiplier is – strictly speaking - zero, as the multiplier seeks to measure economic impact relative to the base-case of no government investment.

5. Conclusion

Partial multipliers are measures that seek to estimate the economic impact of a particular change, and subsequent changes, in the economy. This economic impact can be measured in terms of employment, output, value added, income or investment.

The underlying logic of a partial multiplier is that an expansion of economic activity (triggered by a purchase or an investment) in one sector of the economy causes other sectors to subsequently expand as well, in a way that would not have happened without the investment. Therefore the economic impact is considered to be the sum of expansion in both the initial sector and other sectors.

Partial multipliers are subject to a number of important conceptual limitations. From an economic perspective, multipliers fail to consider the importance of opportunity cost, may be subject to double- and triple counting, and do not distinguish between average and marginal impacts. From a financial perspective they do not take account of the presence of negative multipliers due to financing requirements. Further, the estimation of partial multipliers is subject to data limitations.

As a result of these conceptual and data limitations, partial multipliers offer little practical guidance for public policy. Further, they do not eliminate the need for rigorous analysis of potential government investment on the basis of market failure and identification of a role for government, and robust assessment of direct benefits and costs.

References

Albanese, A., (2008), Minister for Infrastructure, Transport, Regional Development and Local Government Speech to the Sydney Institute, 10 September, Sydney. <http://www.minister.infrastructure.gov.au/aa/speeches/2008/AS21_2008.htm>

Archer, B. H., (1976), ‘The Uses and Abuses of Multipliers’, in Planning for Tourism Development: Quantitative Approaches, eds. Charles E. Gearing, William W. Stewart, and Turgut Var. New York, Praeger Publishers, pp. 115-

132.

Australian Bureau of Statistics (ABS) (1995), Information Paper Australian National Accounts Introduction to Input-Output Multipliers 1989-90, Cat. No. 5246.0, ABS Canberra.

<http://www.abs.gov.au/AUSSTATS/abs@.nsf/DetailsPage/5246.01989-90?OpenDocument>

Australian Bureau of Statistics (ABS) (2008), Australian National Accounts: Input-Output Tables - Electronic Publication, 2004-05 Final, Cat. No. 5209.0.55.001, ABS Canberra.

<http://www.abs.gov.au/AUSSTATS/abs@.nsf/Lookup/5209.0.55.001Main+Features12004-05%20Final?OpenDocument>

Banks, G., (2002), ‘Inter-state bidding wars: calling a truce’, Speech to the Committee of Economic Development of Australia, 6 November, Brisbane.

<http://www.pc.gov.au/__data/assets/pdf_file/0018/7812/cs20021106.pdf>

Campbell, H. (1997), ‘Deadweight Loss and the Cost of Public Funds in Australia’, Agenda, 4 (2), pp. 231-236.

<http://epress.anu.edu.au/agenda/004/02/4-2-NT-3.pdf>

Coughlin, C.C. and T.M. Mandelbaum, (1991), ‘A Consumer’s Guide to Regional Economic Multipliers’, The Federal Reserve Bank of St Louis Review, 73 (1), pp. 19-32.

Department of Finance (2006), Handbook of Cost Benefit Analysis, Financial Management Reference Material, No. 6, January.

<http://www.finance.gov.au/publications/finance-circulars/2006/docs/

Handbook_of_CB_analysis.pdf>

Green, P., (2006), ‘Progress in restoring our environment’ paper prepared for the 2006 Australian State of the Environment Committee, Department of the Environment and Heritage, Canberra.

<http://www.environment.gov.au/soe/2006/publications/emerging/nrm-progress/pubs/nrm-progress.pdf>

Gretton, P., (2005), ‘Australian Input-Output Tables’, Australian Economic Review, Vol. 38 (3), pp. 319-332.

Henry, K., (2007), ‘Treasury’s Investment in the Current Environment: Address to Staff at the Hyatt’, Canberra.

<http://www.treasury.gov.au/documents/1249/PDF/speech_14_march_2007.pdf>

Madden, C., (2001), ‘Using ‘economic’ impact studies in arts and cultural advocacy: A cautionary note’. Media International Australia incorporating Culture and Policy, 98, pp. 161-178.

Minerals Council of Australia (2008), ‘Employment’, <http://www.minerals.org.au/victoria/about_industry/industry_status>

[viewed 1 December]

Sinden, J.A. and D.J. Thampapillai, (1995), Introduction to Benefit-Cost Analysis, Longman, Sydney.

Stevens, B.H. and Lahr, M.L. (1988), ‘Regional Economic Multipliers: Definition, Measurement and Application’, Economic Development Quarterly, 2 (1), pp. 88-96.

Stonecash, R.E., J. Gans, S. King, and N.G. Mankiw, (2003), Principles of Macreconomics, Thomson, Australia.

Victoria Auditor General’s Office (VAGO) (2002), Investment Attraction and Facilitation in Victoria, Melbourne.

<http://download.audit.vic.gov.au/files/Investment_report.pdf>

Victoria Auditor General’s office (VAGO) (2007), State Investment in Major Events, Melbourne.

<http://archive.audit.vic.gov.au/reports_par/agp119_majorevents_report.pdf>

[1] The authors acknowledge valuable input and comment from members of Policy and Strategy Group including Deborah Peterson - Deputy Secretary, Bob Douglas – Chief Economist, Bill Malcolm – Principal Economic Policy Advisor, Anna Heaney – Principal Economic Policy Advisor, Bill Fisher – Principal Economist, Arthur Ha – Principal Economist, Mark Taylor – Manager Statistical Information, and John Rakopoulos – ABS Officer. Correspondence should be directed to: Ismo.Rama@dpi.vic.gov.au.

[2] Partial multipliers are sometimes referred to as regional multipliers, however we avoid this term as it may unintentionally imply a multiplier applied to a non-urban context.

[3] These examples are illustrative only - this note does not provide an analysis of these particular multipliers.

[5] Archer (1976) includes discussion of alternative approaches to calculating mutlipliers.

[6] See ABS (1995) and Gretton (2005) for an overview of input-output tables and associated multipliers produced by the Australian Bureau of Statistics.

[7] Economic analysis is focussed on flows of real resources through the economy, while financial analysis is focussed of financial/accounting flows. While the two are related, it can helpful to distinguish them conceptually.

[8] In a case where resources are drawn from a higher-value use, the partial multiplier may be negative.

[9] Further, if resources are subject to permanent unemployment, more direct policy tools may be able to address such issues more efficiently than particular investment projects.

[10] Output multipliers may be at greater risk of double counting than value added multipliers.

[11] Example adapted from Sinden and Thampapillai (1995).

[12] This hypothetical example also assumes that the claimed secondary benefits are produced using existing resources in the steel and car industries. If new investment is required to increase output in these industries, then this should be considered as part of the cost of the overall project.

[13] Namely, jobs drawn from a pool of permanently unemployed labour.

[14] Many multipliers assume for simplicity that the average and marginal impacts are identical (Archer, 1976).

[15] Where projects are funded from tax revenues there will be further costs to the economy arising from collection and compliance, and arising from tax-induced changes in incentives to work, consume and invest. For a discussion see Campbell (1997) and Banks (2002).