Australasian Agribusiness Review - Vol.15 - 2007
Paper 4
ISSN 1442-6951
Rationalising Risk Assessment: Applications to Agricultural Business*
J Brian Hardaker and Gudbrand Lien
J Brian Hardaker, School of Economics, University of New England, Armidale, NSW
Gudbrand Lien, Norwegian Agricultural Economics Research Institute, Oslo, Norway and Hedmark University College, Rena, Norway
Abstract
To concentrate on treating the most serious risks, methods of business risk management usually seek to identify the main risks and to assess their relative importance. Risks are typically assessed in terms of their chances of occurrence and the severity of their consequences. The assessments may be performed by qualitative, semi-quantitative or quantitative analysis. This paper is focussed on quantitative methods, requiring assessments of specific probabilities and values for consequences.
There are problems with conventional risk assessment. For some risks there may be no specific adverse event. And often the severity of possible adverse consequences is uncertain. Typically, neither the decision maker’s risk aversion nor possible upside outcomes are taken into account. Moreover, the usual one-at-a time approach means that stochastic dependencies and scope for risk spreading through diversification are also ignored.
Risk assessment by certainty equivalents of losses (CELs) is proposed to overcome some of the above-mentioned limitations. The calculation of the CELs is explained and illustrated with agricultural business examples, before limitations of downside risk assessments and the effects of ignoring upside benefits are addressed. An extension of the approach to a portfolio setting is described which accounts for stochastic dependencies and diversification benefits. The suggested approach is extended to deal with the risk of bankruptcy.
Introduction
Any discussion of risk assessment methods confronts the problem that there are many expositions of how to do the task. We have chosen to base what follows mainly on the joint Australian and New Zealand Standard for Risk Management (AS/NZS, 2004a, 2004b), which has been developed after considerable consultation and has attracted international interest. In addition, since we focus on quantitative methods of risk assessment, we have also drawn on Bowden et al. (2001), who provide a detailed description of one approach to quantitative risk assessment, chiefly in a business setting. Their method is essentially an extension of the AS/NZS approach.
After some preliminary steps to clarify the specific context of the assessment process, the methods typically involve identifying and listing the risks which might afflict an organisation, then moving on to an assessment of the relative importance of these risks in order to allow them to be ranked. These steps lead logically to a consideration of ways to manage or treat what are judged to be the most serious risks.
In this paper we examine the merits and limitations of the conventional approach to assessing risks and consider how to improve the process of risk ranking. We focus on agricultural business risks because the business of agriculture is often thought to be especially exposed to risk. Farming in particular is an interesting case because the small size and family ownership of many farm businesses mean that the decision maker’s degree of risk aversion comes more strongly into consideration in risk assessments than in larger scale operations (Eeckhoudt & Gollier, 1995, p. 44).
We argue that the widely recommended approach to risk assessment has some significant limitations. These include a common failure to deal consistently with risk aversion, too strong a focus on downside risk with no consideration of upside benefits, and too little attention to the place of individual risks in the portfolio of risky prospects that together comprise the totality of any business. We show how these limitations might be overcome using standard methods of decision analysis.
Approaches to Risk Assessment
In the conventional approach, risk assessment and ranking is done by considering both the ‘likelihood’ of the risky event (which we shall call ‘probability’ in what follows) and the seriousness of the consequences. These assessments may be performed by qualitative, semi-quantitative or quantitative analysis (AS/NZS, 2004a, section 3.4.4).
In qualitative analysis the probabilities and consequences are described in words, without assigning any numerical magnitudes to either. Rather the considered risks may be assessed using descriptive terms for the probability of each event and the significance of the associated adverse consequences (e.g., Fletcher, 2005). The problem with this method is that the terms chosen as descriptors are unlikely to be interpreted consistently, even though pains may be taken to define their intended meanings. What is to be deduced by such terms as ‘unlikely’ or ‘very unlikely’ to describe probabilities, and ‘serious’ or ‘very serious’ to describe consequences? Obviously, this approach is subject to some imprecision that limits the subsequent use of the judgments in decisions about the relative importance of different risks.
In semi-quantitative analysis, the risks are categorised using quantitative scales but specific values for the probability and consequences of some particular risk are not assessed. Rather the probabilities and consequences are assigned to classes described by approximate numerical values or intervals (e.g., Mellor et al., 2004). Thus, two risks with probabilities of ‘around 0.001’ and with losses of ‘between one and two million dollars’ could in fact be quite different, especially if the defined classes are broad. So, while not quite as vague as the qualitative approach, there is still considerable imprecision in this method which could be problematic in assessing the relative size of different risks consistently.
In quantitative analysis, an effort is made to define specific probabilities and values for consequences. That is obviously more demanding for the analysts but, where it can work, gives a more logical basis for forming conclusions. In what follows we deal only with quantitative analysis. However, some of the difficulties we identify in the implementation of the quantitative methods also apply to the other two approaches. Similarly, the principles underlying our proposed improvements could also be useful for approaches based on qualitative and semi-quantitative risk assessments
Our focus is on business risks which we assume can be adequately described in terms of dollar consequences. Of course, there will often be other dimensions of consequences for some agricultural risks. For example, the risk of flooding of a low-lying farming area will not only cause financial losses but can have social, environmental and animal welfare consequences, among others. Bowden et al. (2001) suggest that non-monetary consequences can often be converted into money amounts. For example, injury to a worker might be valued by the compensation payments that would be paid (whether or not paid by the business itself). Similarly, environmental damage could be valued by the costs of restoration (again whether or not paid by the business). Otherwise, economists have developed some methods for valuing multi-attributed consequence (e.g., Keeney & Raiffa, 1976; Bennett et al., 2002), although the difficulty entailed should not be under-estimated. For simplicity of exposition, we assume in what follows that any non-monetary consequences of risks can converted to money amounts via some acceptable trade-off method.
Measuring the Size of Risks – An Expected Utility Approach
In the approach described in the Australian/New Zealand Standard, individual risks are identified and assessed for ranking purposes. Once the probabilities and consequences of the main risks have been determined, the next step in risk assessment is typically to find some way of combining these assessments into a measure of the relative importance of each risk. In quantitative analysis this may be done by multiplying the probability of each risk by the associated loss. Recognising that there may be a distribution of losses, we choose to call the result of such multiplication the expected loss, although it is given other less satisfactory names in the literature, such as ‘risk’ (AS/NZS, 2004a, 2004b) or ‘risk quotient’ (Bowden et al., 2001). However, we argue below that expected loss alone may not tell the whole story.
Because many decision makers are risk averse, implying increasing marginal disutility as losses increases, it is logical to adjust the expected value for risk aversion. In AS/NZS (2004b) it is proposed that a weighting factor could be included to scale the calculated expected loss, or that an exponential operator be applied to the probability or level of losses, or both. The basis for determining the nature and magnitudes of such adjustments is not explained. However, the subjective expected utility (SEU) hypothesis, on which decision analysis is founded, provides a logical basis for making these adjustments. The hypothesis implies that a decision maker’s attitude to risk is reflected in their utility function for consequences. Therefore, it we can get a measure of the shape of this function for a particular decision maker, we can use this estimate of their attitude to risk to evaluate and rank different risks for that person. Raiffa (1968, ch. 9) provides a good review of the pros and cons of the decision analysis approach to risky business decision making. Applications to agricultural business decision are discussed in Anderson et al. (1977) and Hardaker et al. (2004a).
It is generally accepted that the degree of risk aversion for a given risk is likely to decrease as wealth increases (Arrow, 1965; Eeckhoudt and Gollier, 1995, p. 45). Therefore, to evaluate the risk of losses requires information about the wealth or equity at risk in the business, as well as about the attitude to risk of the decision maker. This information is then combined with estimates of the loss and its associated probability or probability distribution.
We illustrate this approach with a simple example. Suppose an Australian farmer is worried about the possibility of losing a niche export market for beef in Japan due to the imposition of quarantine restrictions following the discovery of BSE (bovine spongiform encephalopathy or ‘mad cow’ disease) in Australia. We assume the farmer assigns a probability of 0.05 to this event (and hence a probability of 1 – 0.05 = 0.95 to the event that the market remains viable). Moreover, he believes that the change will be irreversible in the short to medium term, so that the loss is calculated as the net present value of lost revenue over the next several years, valued at $800,000. We can represent this risk in the following payoff table:
Event |
Probability |
Loss ($) |
Loss of market |
0.05 |
800,000 |
Market retained |
0.95 |
0 |
Expected loss |
40,000 |
To evaluate this risk we need to know how large the loss of $800,000 is, relative to the net assets of the farm business, and also how risk averse the farmer is. We assume that the net assets are $4 million. Thus, the risk can be redefined in terms of terminal equity or wealth, as follows:
Event |
Probability |
Wealth after loss |
Loss of market |
0.05 |
3,200,000 |
Market retained |
0.95 |
4,000,000 |
Expected wealth after loss |
3,960,000 |
Note that, in taking this step, we are assuming ‘asset integration’, meaning, in this context, that the farmer is willing to view the loss that might occur as a change in wealth. Such asset integration makes sense particularly for prescriptive decision analysis (Hardaker, 2006), which is usually applicable in risk assessment.
In assessing the risk attitude of the farmer with respect to wealth, we start with the following categories, proposed by Anderson & Dillon (1992):
Description |
Relative risk aversion |
Hardly risk averse at all |
0.5 |
Somewhat risk averse (normal) |
1.0 |
Rather risk averse |
2.0 |
Very risk averse |
3.0 |
Extremely risk averse |
4.0 |
The categorisation is in terms of relative risk aversion coefficients because these are pure numbers and so are comparable for risks evaluated in different currency units (or multiples thereof).
Suppose our farmer is initially categorised as ‘rather risk averse’ with a relative risk aversion coefficient with respect to wealth of 2.0. We now calculate the certainty equivalent loss (CEL) of the risk to be faced. This is the sure sum that has the same utility for the farmer as the expected utility of facing the risk (e.g., Keeney & Raiffa, 1976). In other words, it is the maximum sure payment that the farmer would be willing to pay rather than face the risk. Certainty equivalents (CEs) were used, by e.g., by Gloy & Baker (2001), as a benchmark for assessing other choice criteria for evaluating risk management strategies.
For risk assessment, we can call the CEL the decision maker’s willingness to pay (WTP) to eliminate the risk. Risks can then be ranked in order of importance using WTP. The steps in the calculation are:
- deduct the losses associated with a given risk from the net assets, as shown above;
- convert the possible future net asset positions to utility values using a constant relative risk aversion (CRRA) utility function (Pratt,1964) with the chosen risk aversion coefficient, in this case 2.0 (see the Appendix for a description of this function);
- compute the expected utility as the probability-weighted average of the utilities of the contingent net assets
((0.05*U($3,200,000) + 0.95*U($4,000,000) = 0.05*-3.125E-07 +0.95*-2.5E-07 = -2.531E-07); - use the reverse utility function to convert the expected utility back to a CE money value
(U-1(-2.531E-07) = $3,950,617); and - deduct the starting net asset value to get the CEL of the risky prospect
($4,000,000 - $3,950,617 = $49,383).
The result in this case is a CEL of $49,383. This is the amount the decision maker would be willing to pay, under the assumptions made, to eliminate the assessed risk and is the appropriate measure of the importance of this risk to the decision maker. The difference between this and the expected money loss of $40,000 of $9,383 is the risk premium and measures the cost of risk aversion under the assumptions made.
The algebra underlying the calculations using the CRRA utility function is provided in the Appendix.
Having found the CEL of the risk specified above, there is now an opportunity to check the assumed risk aversion coefficient. The decision maker should be indifferent between a 0.05 probability of a $800,000 reduction in present value of future earnings and paying what can be thought of as a once-only insurance premium of $49,383 to eliminate the possible loss. If this is not so, the assumed risk aversion coefficient can be adjusted to match the actual amount he would be willing to pay to avoid the risk. To help in this process, akin to the method of stochastic efficiency analysis called SERF (Hardaker et al., 2004b), we can vary the coefficient of relative risk aversion over the plausible range to produce the graph shown in Figure 1.
Figure 1. Analysis of the risk of loss of a Japanese export market for a range of degrees of risk aversion

With some introspection, the farmer, perhaps with the help of the adviser, may be able to use the information in this graph to refine the original assumption about what degree of risk aversion is appropriate for him. The introspective task involves only one possible loss with an associated probability, so is less challenging than some more complex situations. And most decision makers are used to making very similar decisions about whether or not to insure some risk for a given premium.
For example, if the decision maker decided that his or her CEL in this case was close to $45,000, that would imply a relative risk aversion coefficient of around 1.0 (somewhat risk averse), which if the decision maker nominated a CEL of about $55,000, the implied risk aversion measure would be close to 3.0 (very risk averse). Once refined in this way, the coefficient of relative risk aversion can be used in the assessment of other risks, some perhaps with multiple possible payoffs, thereby assuring consistency of assessments across different risks.
When the actual degree of risk aversion of the decision maker is not known, for whatever reason, it is possible to use the graphical analysis illustrated in Figure 1 to compare risks. As with SERF, such a comparison will generally produce only a partial ordering of the risks, in that some curves may cross, implying that the ranking of those risks is dependent on the actual degree of risk aversion of the decision maker.
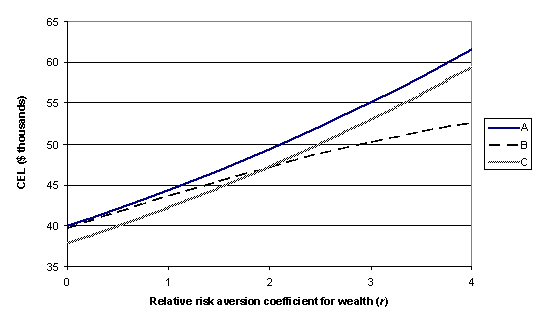
For example, in Figure 2 the risk above, denoted as A, is compared with two other risks, B and C. It is clear that A is the most important of the three at all levels of risk aversion in the plausible range. However, B ranks above C in importance for relative risk aversion below about 1.9, with C a more significant risk than B for more risk-averse decision makers.
Figure 2. Comparison of three risks of loss, A, B and C, for a range of degrees of risk aversion
A Case with Uncertain Losses
Even when specific events or sequences of events that constitute ‘risks’ have been identified, the magnitude and severity of the consequences may be uncertain, perhaps because they could vary from case to case, or merely because of uncertainty in deciding what might happen. That implies a need to specify a probability distribution of possible consequences for many, perhaps most risks (conditional upon the adverse event(s) occurring). This need is recognised in some but not all expositions of how to undertake risk assessment. The method of measuring the size of risks described above is readily extended to cases with a probability distribution of losses.
To illustrate, we now suppose that the same farmer views the risk of loss of the export market not as a simple yes/no risk but with a range of possible extents to which the market is reduced, as set out in Table 1.
Table 1. Farmer’s assessment of possible market reductions in net present value terms
Event |
Probability |
Loss ($) |
Loss of 100% of market |
0.02 |
800,000 |
Loss of 75% |
0.02 |
600,000 |
Loss of 50% |
0.02 |
400,000 |
Loss of 25% |
0.02 |
200,000 |
No loss |
0.92 |
0 |
Expected loss |
40,000 |
Although the numbers have been chosen so that the expected loss is the same as in the earlier case, the WTP to eliminate these possible losses is now reduced somewhat to $46,666 at a relative risk aversion level of 2.0 as used before. The smaller WTP arises because of the possibility that the loss will be less than assumed before.
Note that the method described deals with a discrete distribution of losses and the example shows only five states. It is trivial to extend the size of the table to deal with as many states as are deemed necessary to give a close representation of the perceived uncertainty of losses.
Dealing with the Risk of Bankruptcy
There are both technical and conceptual issues to be addressed if the maximum possible loss is greater than the equity capital of the business. The CRRA function is undefined for non-positive wealth and in any case it does not make sense to try to measure the utility of negative wealth since it is unlikely that a business could persist with negative equity. The solution we propose is to consider what actually happens if a business suffers a catastrophic loss that drives it into bankruptcy.
We consider first the case of a family-owned firm. While bankruptcy may spell the end of the business, it does not signal the end of the family. Not all of the family capital is confiscated after bankruptcy. In particular, the human capital of the family members is retained, along with such other assets as are protected from resumption by local laws and practices. For example, it is usual for bankrupts to be allowed to retain personal effects and perhaps some assets needed for a normal life and employment such as motor vehicles and tools. So there can be considerable family wealth not at risk, which might best be assessed as the CE of the capitalised value of the family’s future consumption after failure of the business. This CE of wealth not at risk represents an assured minimum asset position for the calculation of expected utility and CEL values in risk evaluation. As Quiggin (1992), noted, the protection of some assets under bankruptcy law acts rather like insurance in limiting the downside losses that can be incurred. The implied horizontal floor to expected utility explains why decision makers become more willing to take risks as bankruptcy threatens.
Assessing wealth not at risk may not be easy. Not only will the future after bankruptcy be uncertain, but there may also be a need to adjust for lost lifestyle benefits and for difficulties the family might face as a result of bankruptcy, such as social stigma and problems in borrowing money in the future. However, it may be possible to make a rough estimate of wealth not at risk, and then to undertake some sensitivity analysis to judge how the results of risk assessment are affected by the value chosen (see Lien et al. (2007) for an illustration).
In the case of a corporate business, while the same general principles would apply, there are extra difficulties in applying the notion of wealth not at risk. The shareholders who own the equity capital at risk are likely to be a diverse group. For some, the loss may be very minor in their overall portfolios. Other investors may have a significant part of their capital at stake. There seems to be no easy way to resolve such diversity other than to meet with the decision makers (senior executives or directors who are appointed to represent the interests of the shareholders) to try to determine how they wish to handle risks of catastrophic losses. However, there may a principal-agent problem in relation to corporate risk of bankruptcy, illustrated by recent events such as the Enron collapse (Munzig, 2003). The company executives generally do not have as much to lose as shareholders if the company faces catastrophic losses so they may be prepared to take risks that shareholders would not wish them to take.
Limitations of Downside Risk Assessment
As AS/NZS (2004a, 2004b) note, many risk analyses focus on the negative consequences of events. Yet managers often decide to expose their businesses to such risks because of the associated upside benefits. So assessing and ranking risks by their downside consequences alone is incomplete and may produce misleading results. Two risky prospects with similar downside consequences may have very different upside outcomes, so that one would be acceptable and the other not.
Moreover, while it is obviously essential for good risk management to think carefully about what might go wrong, adverse consequences may not flow from readily identifiable causal events. Rather they may be the outcome of the unfortunate conjunction of several, perhaps many, events, none of which, considered in isolation, may have been identifiable ex ante as a potentially significant risk. In farming, for example, a period of somewhat low yields and poor prices, coupled with rising costs, might be enough to cause a marginal farm business to fail, yet perhaps none of the factors contributing to that failure could have been traced to specific identifiable adverse events. Even if, say, a low yield of wheat, or a low price for barley, or a high price of fuel were to be viewed as risky events, how could the associated ‘losses’ be assessed? i.e. relative to what ‘no risk’ or ‘normal’ situation would ‘losses’ be measured, given that yields, prices and costs are always uncertain? Indeed, the implication in the common view that risks are in some way abnormal events that disturb the otherwise more or less riskless operation of the business is unrealistic and sometimes unhelpful.
Consider the case of an Australian farmer who is deciding what enterprise program to adopt in the coming year on part of the farm covering 400 ha. For simplicity, we assume there are only two enterprises, wether sheep for wool or winter wheat, and that the whole of the 400 ha would be devoted to one or the other. The farm has a total area of 1000 ha and the farmer’s net asset position is $1 million. We again assume a relative risk aversion coefficient for wealth of 2.0. We also assume that yields and prices are the only uncertain quantities that need to be taken into account in this risk assessment. Although the average levels of performance were based on data from NSW Department of Primary Industries, for lack of any relevant historical data, the uncertainties to be faced were quantified using imaginary values. The resulting marginal probability distributions for each stochastic variable are summarised in Table 2.
Table 2. Summary statistics of yield and price distributions for the cropping choice decision
Yields |
Prices |
|||
Wool kg/hd |
Wheat t/ha |
Wool $/kg |
Wheat $/t |
|
Mean |
6.08 |
2.79 |
4.54 |
191.8 |
StDev |
1.87 |
1.39 |
0.93 |
63.8 |
CV % |
30.76 |
49.91 |
20.41 |
33.3 |
Min |
2.30 |
0.00 |
2.40 |
90.0 |
Max |
9.50 |
5.29 |
6.00 |
329.7 |
It is assumed that for neither product is there any correlation between yields and prices at farm level.
The budgets used to compare the two cropping scenarios are given in Table 3 for wethers and in Table 4 for wheat. In both cases, the stochastic variables are set at their expected values.
Table 3. Expected per ha gross margin for wethers
Wethers for wool |
|||||
Income/100 head |
no |
kg/hd |
$/kg |
||
Wool |
98 |
6.08 |
4.54 |
$2,704 |
|
Crutchings |
99 |
0.25 |
2.61 |
$64 |
|
Wool income |
$2,768 |
||||
Less livestock depreciation |
$293 |
||||
Net income/100 head |
$2,476 |
||||
Variable costs/100 head |
$1,273 |
||||
Gross margin/100 head |
$1,203 |
||||
Stocking rate/ha |
10 |
||||
Gross margin/ha |
$120.26 |
||||
Based on farm enterprise budget from NSW DPI |
|||||
Merino wethers 21 micron |
|||||
Table 4. Expected per ha gross margin for wheat
Wheat |
|||
t/ha |
$/t |
$/ha |
|
Wheat income/ha |
2.79 |
191.82 |
$534 |
Variable costs/ha |
$308 |
||
Gross margin/ha |
$226 |
||
Based on farm enterprise budget from NSW DPI |
|||
Short-fallow wheat Central Zone East |
|||
Note that, because yields and prices are stochastic, gross margins are also stochastic. Since this is an annual model, it is convenient to make the evaluation in terms of income, not wealth. For this purpose, we use a constant absolute risk aversion (CARA) utility function with the effect of the existing level of the farmer’s wealth accounted for by deriving the coefficient of absolute risk aversion as a = r/W = 2.0/4,000,000, where r is the relative risk aversion coefficient. The CARA function is detailed in the Appendix where its use in this application is justified.
The two land-use scenarios were simulated in the Excel add-in software package Simetar (www.simetar.com) using Latin hypercube sampling for 1000 iterations to estimate the probability distributions of net income for each scenario. The resulting cumulative distribution functions are shown in Figure 3.
Figure 3. Comparison of two land-use scenarios (400 ha wheat vs. 4000 wethers)
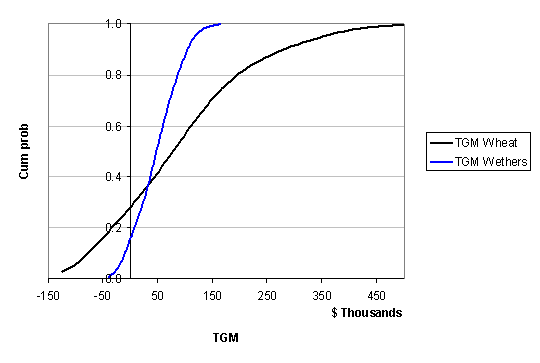
As the graphs in Figure 3 show, the wheat scenario has the higher probability of loss. The following results confirm that, by three different loss criteria, the wheat is inferior to wethers:
Scenario |
Wheat |
Wethers |
Probability of a loss |
27.8% |
16.1% |
Expected loss ($) |
58,661 |
13,522 |
CE of loss (r = 2) ($) |
59,797 |
13,618 |
Bold indicates loss minimisation.
By contrast, if we now examine the full distributions of results in overall risk efficiency terms, the ranking of the two scenarios is reversed:
Scenario |
Wheat |
Wethers |
Expected TGM ($) |
90,166 |
48,130 |
CE of TGM (r = 2) ($) |
73,820 |
46,427 |
Bold indicates risk efficiency.
In this case, whether in terms of expected value or for a relative risk aversion coefficient of 2, the wheat scenario is clearly better than running wethers on the 400 ha.
The coefficient of relative risk aversion in the above analysis of 2.0 fits into the category of ‘rather risk averse’ as set out above. In Figure 4 we illustrate the effect on CE of varying the coefficient of relative risk aversion over the full plausible range.
Figure 4. CEs of total gross margin for the land-use scenarios (400 ha wheat vs. 4000 wethers)
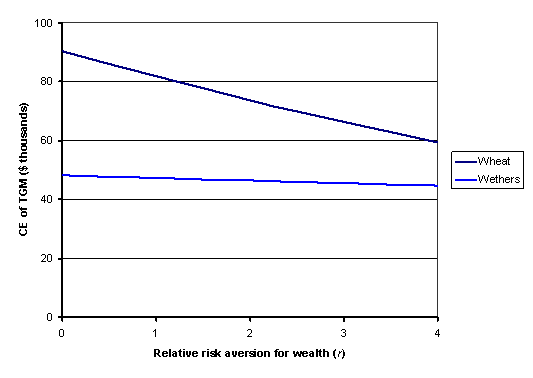
As Figure 4 shows, at no plausible level of risk aversion is the scenario of running wethers superior to that of wheat production, emphasising that a focus on losses alone can be seriously misleading in decisions such as this.
The Case for a Portfolio Approach
Focussing only on losses may also be misleading in that some risks are more easily ‘treated’ than others. For example, insurable risks are more easily managed than those that are not insurable. Differences in upside consequences and in the scope to ameliorate some risks need to be explored in the planning stage of risk management. The subjective expected utility model outlined above can be applied to such planning decisions. To illustrate, we look at the use of insurance in the next example, again focusing on the willingness to pay to avoid risk, here defined as levels of revenue below a specified proportion of the corresponding expected values.
Partial assessment of risky prospects as illustrated so far in this paper is based on an implicit but strong assumption that there is no stochastic dependency (e.g. no positive or negative correlation) between the various risks. But that is unlikely to be true for many risky prospects. In agriculture, crop yields tend to be positively correlated in that a good year for one crop also often suits other crops, and vice versa. Similarly, prices for several kinds of farm products tend to move together, depending on general economic conditions. Ignoring stochastic dependency between risky prospects can be seriously misleading.
Similarly, looking at risks one at a time ignores the benefits from diversification. Provided risks are less than perfectly correlated, there is potential for diversification to improve risk efficiency and so to reduce the ‘costs’ of individual risks. These benefits can only be assessed in a whole-firm context.
Methods of treating risk can usually readily be incorporated into a firm-level portfolio selection model, such as quadratic mean-variance (EV) model or a utility efficient (UE) formulation (Lambert & McCarl, 1985; Patten et al., 1988). Such models can be formulated and solved with a specific risk or group of risks left untreated, and then solved again assuming these risks are treated to eliminate them. The difference in CEs between the two solutions, for the degree of risk aversion of the decision maker, measures the importance of the risks considered in terms of CEL (= WTP) values. The same models can also be used to show which risky prospects should be taken up and which not, as well as showing which risks should be managed within the firm and which should be handled by trading away some of the risk, e.g. by purchase of insurance or derivatives.
We illustrate the portfolio approach with a simplified example, chosen for ease of presentation rather than realism. An imaginary crop farm in NSW with a land area of 1000 ha grows three crops: barley, wheat and canola. We assume that we have historical information from the farm sufficient to define nine equi-probable discrete states of nature in terms of crop yields and prices. As well as the limited land area, the cropping program is constrained by crop rotational limits and a labour constraint. The farmer is again assumed to have a relative risk aversion coefficient of 2.0 and net assets of $1 million.
Since we are modelling impacts on next year’s income, we again choose to use a constant absolute risk aversion (CARA) utility function. That validates the comparison of change in CE with willingness to pay for insurance, i.e. CE with indemnity minus CE without is equal to WTP for insurance. As before, we derived the coefficient of absolute risk aversion as a = r/W = 2.0/1,000,000, where r is the relative risk aversion coefficient.
The information above was built into a UE programming model in Excel which was solved by the standard Excel add-in called Solver. The objective function was defined to maximise the CE of the stochastic farm total gross margin. (Using the CARA function, not accounting for fixed costs makes no difference to the calculated WTP values.)
The only risks appraised in this illustration are the risks of low crop revenues due to poor yields and/or low prices. We defined an outcome where the crop revenue is less than 80 per cent of the expected value as ‘adverse’. We chose this value as it may be possible to insure against such outcomes, whereas it unlikely to be sensible or feasible to insure any higher proportion of expected returns. We evaluated the risks crop by crop, for all three crops and for total crop revenue. The importance of each risk is judged by assessing the farmer’s WTP to eliminate it, calculated as the difference between CEs with and without risk protection. This is the maximum amount the farmer would be willing to pay to buy insurance to protect against each risk. Results are summarised in Table 5.
Table 5. UE programming solutions for various revenue protection options
Protection option |
CE |
Barley |
Wheat |
Canola |
WTP |
$ |
ha |
ha |
ha |
$ |
|
Nil |
73,067 |
238 |
400 |
333 |
|
Barley |
79,037 |
353 |
313 |
333 |
5,970 |
Wheat |
74,478 |
238 |
400 |
333 |
1,411 |
Canola |
89,014 |
238 |
400 |
333 |
15,947 |
All 3 crops |
96,058 |
353 |
313 |
333 |
22,991 |
Total revenue |
87,018 |
353 |
313 |
333 |
13,951 |
Only two of the risk protection options - barley insurance and insurance of all three crops - have an effect on the cropping pattern. But all risk protection options lead to some differences in the CEs of income. The WTP information shows that the most significant crop revenue risk is for canola. Protecting the revenue of all three crops leads to a smaller WTP than the sum of protecting each one individually, presumably because of the scope to reduce risk by growing less of the more risky wheat relative to barley. But the most significant result is that crop revenue protection has a smaller WTP than protecting the three crops individually, because of the benefits from diversification. Moreover, the indemnity payments an insurer would have to pay to the farmer to eliminate risk at this level of aggregation (not shown in the table) are much lower, making this the most viable option for a successful commercial insurance deal to be struck.
There are some important limitations to this simplified example, so that the results should be treated with caution. The small number of constraints and activities in the model mean that the solution is relatively insensitive to changed assumptions. In more realistic modelling we would expect to see more changes in the farm land-use patterns as different risk management options are introduced. Moreover, to account for risk in crop returns with reasonable accuracy, a much larger number of states of nature would be preferable. We could generate more states in a real application to overcome this problem, for example using the method of multivariate kernel smoothing of sparse data suggested by Richardson et al. (2006), followed by Latin hypercube simulation to generate, say, 100 states.
Despite its limitations, however, the model results do illustrate how risk assessment can be conducted in a portfolio setting. The results show not only which risks matter, but also what could be afforded to treat those risks by buying crop revenue insurance, if available. It would be possible, at least in principle, to extend the model to include options to buy other risk-sharing instruments, such as growing crops under contract, crop yield insurance, commodity price futures or weather derivatives, to find the best way of treating the risks.
Conclusions
It makes sense in risk assessment to look at what can go wrong in the operation of a business or other organisation and to try to focus on those risks that really matter. These will be the ones with non-trivial probabilities of occurrence and with potentially serious consequences. However, sorting out which risks matter using non-quantitative or semi-quantitative methods may lead to ambiguous conclusions. Even with quantitative assessments, the typical absence in commonly advocated methods of a systematic way to accommodate risk aversion seems unsatisfactory. The method of assessment by CELs proposed here overcomes these limitations. In applying the method, it will sometimes be necessary to deal with the risk of business failure due to catastrophic losses, and a procedure for dealing with that eventuality is suggested.
In addition, however, the conventional approach may not tell the whole story. Not all bad outcomes can be linked to some clear adverse event or sequence of such events. Often it will be more productive to focus on the distributions of possible risky outcomes which, in farming as in other forms of business, may be due to many causes, such as unpredictable weather or prices, or the whims of political decision makers. Moreover, a focus on losses alone may also be misleading, since, as illustrated, differences in upside consequences can lead to different assessments of the relative importance of risky prospects. And looking only at losses tells nothing about which risks should be treated, by what means.
For many risks, such as those arising from weather or price instability, there is a need to account for possible stochastic dependencies, including consideration of the benefits to be had from risk spreading via diversification. Hence, it may not be sensible to look at risks and their possible treatment on a partial or one-at-a-time basis. Rather it will often be wise to assess risks and to analyse the choice among alternative courses of action within a whole-firm portfolio planning context, as is possible using mathematical programming methods.
Appendix on Utility Functions Used
The CRRA function is generally appropriate for the evaluation of risks with wide variation in wealth, partly because it exhibits decreasing absolute risk aversion as wealth increases. The modified power function used is of the form:
U = {[1/(1 – r)]}W (1- r) (1)
where U is utility, r is the relative risk aversion coefficient, assumed constant, and W is net assets or wealth. Expected utility (EU) is then found as the probability-weighted value of the utilities of the possible loss or losses. The reverse form of (1) to derive the certainty equivalent value of wealth is:
CE (W) = [EU(1 – r)]{1/(1 – r)} (2)
The power function is replaced by a log function when relative risk aversion is 1.0, i.e.:
U = ln (W) (3)
The reverse form of (3) to find CE from expected utility is:
CE (W) = exp (EU) (4)
The CARA (negative exponential) utility function for net income is relevant for evaluating more marginal risky prospects which are small relative to the equity of the business, such as risks affecting only next year’s income. In such applications the CARA function is preferred for four main reasons: (1) The CRRA function is undefined for negative payoffs, so cannot be used in cases where losses can occur. (2) The property of constant absolute risk aversion, considered unrealistic when analysing risks that threaten the asset base, is less concerning when the range of outcomes is small, i.e. constant absolute risk aversion is likely to be a reasonable approximation to the actual but usually unknown attitude to risk. (3) Like the CRRA function, the CARA function has a single coefficient of risk aversion, making it more convenient to use than some other alternatives. (4) As Kallberg & Ziemba (1983) and Lien and Hardaker (2001) illustrate, for risks with payoffs that are small relative to wealth, choice of functional form can be expected to have a negligible effect on CE values, provided the degree of risk aversion is represented consistently.
The form of the CARA function is:
U = 1 – exp(–aX) (5)
where X is transitory income or change in income and a is the coefficient of absolute risk aversion. The value of a can be got from the coefficient of relative risk aversion by the formula:
a = r/W (6)
The reverse of equation (5) is:
CE (X) = –ln (1 – EU)/a (7)
References
Arrow, K.J. (1965), Aspects of the Theory of Risk-Bearing, Yrjö Jahnssonin Säätiö, Academic Bookstore, Helsinki.
AS/NZS (2004a), Risk Management, Standard AS/NZS 4360:2004, Australian Standards and New Zealand Standards.
AS/NZS (2004b), Risk Management Guidelines: Companion to AS/NZS 4360:2004, Handbook HB436:2004, Australian Standards and New Zealand Standards.
Anderson, J.R., & Dillon, J.L. (1992), Risk Analysis in Dryland Farming Systems, FAO.
Anderson, J.R., Dillon, J.L., & Hardaker, J.B. (1977), Agricultural Decision Analysis, Iowa State University Press.
Bennett, J., Blamey, R., Louivere, J., & Morrison, M. (2002), “Choice modelling and tests of benefit transfer”, American Journal of Agricultural Economics, 84, 161-70.
Bowden, A.R., Lane, M.R., & Martin, J.H. (2001), Triple Bottom Line Risk Management, Wiley.
Eeckhoudt, L., & Gollier, C. (1995), Risk: Evaluation, Management and Sharing, Harvester Wheatsheaf.
Fletcher W.J. (2005), “The application of qualitative risk assessment methodology to prioritize issues for fisheries management”, ICES Journal of Marine Science, 62, 1576-1587.
Gloy, B.A., & Baker, T.G. (2001), “A comparison of criteria for evaluating risk management strategies”, Agricultural Finance Review, 61, 37-56.
Hardaker, J.B. (2006), “Farm risk management: past, present and prospects”, Journal of Farm Management, 12 (10), 593-612.
Hardaker, J.B., Huirne, R.M.B., Anderson, J.R., & Lien, G. (2004a), Coping with Risk in Agriculture, 2nd edn, CAB International.
Hardaker, J.B., Richardson, J.W., Lien, G., & Schumann, K.D. (2004b), “Stochastic efficiency analysis with risk aversion bounds: A simplified approach”, Australian Journal of Agricultural Economics, 48, 253-70.
Kallberg, J.G., & Ziemba, W.T. (1983), “Comparison of alternative utility functions in portfolio selection problems”. Management Science, 29, 1257-1276.
Keeney, R.L., & Raiffa, H. (1976), Decisions with Multiple Objectives: Preferences and Value Tradeoffs, Wiley.
Lambert, D.K., & McCarl, B.A. (1985), “Risk modeling using direct solution of nonlinear approximations of the utility function”, American Journal of Agricultural Economics, 67, 846-852.
Lien, G., & Hardaker, J.B. (2001), “Whole-farm planning under uncertainty: impacts of subsidy scheme and utility function on portfolio choice in Norwegian agriculture”, European Review of Agricultural Economics, 28, 17-36.
Lien, G., Hardaker, J.B., & Flaten, O. (2007), “Risk and economic sustainability of crop farming systems”, Agricultural Systems, 94, 541‑552.
Mellor, D.J., Innocent, G.T., McEwen, S.A., Reilly, W.J., Taylor, D.J., Steele, W.B., Gunn, G.J., Ternent, H.E. & Reid, S.W.J. (2004), “A semi-quantitative risk assessment model for contamination of beef carcasses with Escherichia coli O157”, in: Food safety assurance and veterinary public health - volume 2 - Safety assurance during food processing, Smulders F.J.M. & Collins J.D. (Eds), Wageningen Academic Publishers, 386-388.
Munzig, P.G. (2003). Enron and the Economics of Corporate Governance. Honor Thesis 2003, Stanford University; Department of Economics. Available at:
www-econ.stanford.edu/academics/Honors_Theses/Theses_2003/Munzig.pdf (last viewed 31 May 2007).
Patten, L.H., Hardaker, J.B., & Pannell, D.J. (1988), “Utility-efficient programming for whole-farm planning”, Australian Journal of Agricultural Economics, 32, 88-97.
Pratt, J.W. (1964), “Risk aversion in the small and in the large”, Econometrica 32, 122-136.
Quiggin, J. (1992), “Some observations on insurance, bankruptcy and input demand”, Journal of Economic Behaviour and Organization, 18, 101‑110.
Raiffa, H. (1968), Decision Analysis, Addison-Wesley.
Richardson, J.W., Lien, G., & Hardaker, J.B. (2006), Simulating multivariate distributions with sparse data: a kernel density smoothing procedure, Paper presented at the 26th International Conference of Agricultural Economics, Gold Cost, Australia, August 12-18, 2006.
Richardson, J.W., Klose, S.L., & Gray, A.W. (2000), “An applied procedure for estimating and simulating multivariate empirical (MVE) probability distributions in farm-level risk assessment and policy analysis”, Journal of Agriculture and Applied Economics, 32, 299-315.