Potential Returns to the Australian Sheep and Wool Industries from Effective R&D and Promotion Investments and their Sensitivities to Assumed Elasticity Values

Australasian Agribusiness Review - Vol.16 - 2008

Paper 1

ISSN 1442-6951

Potential Returns to the Australian Sheep and Wool Industries from Effective R&D and Promotion Investments and their Sensitivities to Assumed Elasticity Values

Stuart Mounter^ab, Garry Griffith^ab, Roley Piggott^a, Euan Fleming^a and Xueyan Zhao^c

a School of Business, Economics and Public Policy, University of New England, Armidale.

b Rural Innovation Branch, NSW Department of Primary Industries, Armidale.

c Department of Econometrics and Business Statistics, Monash University, Clayton.

Abstract

In recent years, Australian sheepmeat and wool producers have been exposed to more volatile and less secure market environments, placing greater pressure on producer-funded investments to be efficient and profitable. Knowledge about the size and distribution of the potential returns from alternative broad types of R&D and promotion investments permits strategic-level decisions about resource allocation, both within and across research programs. This is particularly important for the Australian sheepmeat and wool industries because they are characterised by strong cross-commodity relationships due to the joint product nature of the industries. Mounter et al. (2007) developed an equilibrium displacement model (EDM) of the Australian sheepmeat and wool industries to account for these relationships and any indirect benefits and costs arising from spill-over and feedback effects between the industries as a result of research-induced innovation or promotion. However, the values for many of the economic parameters in the EDM had to be specified subjectively due to the absence of relevant empirical estimates. Uncertainty about true parameter values raises concerns over the robustness of the results generated from the EDM. In this paper we use the EDM to estimate the potential annual returns and their distribution among the various industry sectors for nine hypothetical investment scenarios. Initially, the EDM is solved for the base set of parameter values. A formal stochastic sensitivity analysis is then undertaken to account for the uncertain parameter values in the model. The results were found to be relatively robust to different parameter values, indicating that the model as specified provides a credible framework to estimate and compare the potential impacts from new technologies, generic promotions and other industry changes in a consistent way.

1. Introduction

Since the collapse of the Reserve Price Scheme for wool in the early 1990s the Australian sheepmeat and wool industries have been faced with a number of challenging issues. Global demand for wool has declined in the face of strong competition from substitute fibres in wool’s traditional apparel markets, and from the ongoing fallout of the destabilisation caused by the Reserve Price Scheme. Lower returns for wool and periods of sustained drought have contributed to sheep numbers falling from 173 million in 1990 to less than 87 million in 2007 (ABARE 2007b). During this time wool production has decreased by more than the decrease in sheep numbers with an increased proportion of ewes and a decreased proportion of wethers in the national flock indicative of a shift in focus towards lamb production (ABARE 2006, 2007a). A sharp decline in Australia’s wool processing industry has arisen from global overcapacity and the emergence of China and other low labour cost regions in wool processing. Welfare concerns over live sheep exports and mulesing to prevent fly strike have featured prominently in media headlines amid animal rights campaigns for boycotts on the purchase of Australian sheep and wool products. Overall, wool and sheepmeat markets are more volatile and less secure than in previous decades.

Significant contributions in the form of compulsory levies on gross wool and livestock sales are made by Australian sheep producers to R&D investments and generic promotions undertaken by industry research providers and organisations such as Australian Wool Innovation (AWI) and Meat and Livestock Australia (MLA). The allocation of funds directed to R&D or promotion has always been a contentious issue. As pointed out by Piggott (1998), Australian woolgrowers and red meat producers have often questioned the level of returns received on the investment of their levy dollars. The current levy rates are 2 per cent on the sale price of greasy shorn wool (AWI 2007) and 2 per cent on sheep and lamb sales. Where there is a defined sale price of $5.00 or more, producers pay 2 per cent of the sale price up to a maximum of $0.20 for sheep and up to a maximum of $1.50 for lambs. If there is no defined sale price the rates are $0.20 and $0.80 for sheep and lambs, respectively. No levies apply to sales of less than $5.00 (MLA 2006). Australian taxpayers also contribute on a dollar-for-dollar basis to the R&D component. According to their respective financial reports, AWI has a total budget of around $60m pa and MLA has a budget for sheep-meat of around $30m pa.

Given the uncertain market conditions confronting the Australian sheepmeat and wool industries, it is imperative that funds made available for R&D and promotion are invested efficiently to maximise net returns to the industries and the community. Reliable information is a fundamental requirement in any decisions regarding levy changes but to date such information has been limited because comprehensive industry models have not been available.

In this paper, an equilibrium displacement model (EDM) developed by Mounter et al. (2007) is used to assess the potential returns to the Australian sheepmeat and wool industries from hypothetical effective R&D or promotion campaigns. This is the same methodology as used in earlier papers published in this Review (Zhao, Griffith and Mullen 2001; Mounter, Griffith and Piggott 2005). Knowing the potential size and distribution of returns from alternative research and promotion investments across different sectors of an industry enables more informed strategic level decisions to be made about how to allocate limited resources among a number of investment options.

Another use of this type of model is ex post analyses of actual technologies that have been researched, developed and adopted. The EDM described in this paper has been used in recent months to evaluate the potential economic returns from the QPLU$ genetic selection technology (Mounter et al. 2008).

One of the problems with economic evaluations of research or promotion expenditures is that, inevitably, they are encumbered by assumptions that may have an influence on results. Assumptions made about price and quantity data, and the values chosen for market parameters, can influence the results generated from the EDM. Errors can also arise from incorrect specifications of demand and supply curve shifts, R&D and adoption lags and numerous other factors. In EDM evaluations, the main concerns focus on the robustness of the calculated benefits when there is uncertainty about the true parameter values. Empirical estimates for some parameters are readily available from the literature though, often, there is disparity among values due to different time periods of estimation and the choice of method or functional form. For other parameters, empirical estimates are scarce or non-existent. In Mounter et al. (2007), subjective judgment provides the basis for the specification of numerous parameter values. Hence, an additional aim of this paper is to account for the responsiveness of the results to errors in the specified parameter values using a formal sensitivity analysis.

2. The Structural Model

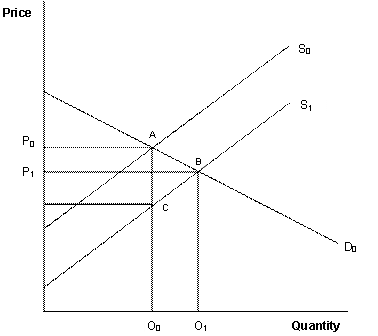
The Australian sheep and wool industries consist of numerous market segments (AWI 2007, MLA 2006). The horizontally and vertically disaggregated framework of an EDM allows for the estimation and comparison of the annual total returns from R&D and promotion investments and their distribution among the various industry sectors and markets. The industry structure is represented by a system of general functional form demand and supply equations defining equilibrium in all markets. The impact of a new technology in an industry sector is modelled as a vertical parallel shift of the supply curve in the market in which the R&D is assumed to occur. A one per cent downward shift represents a one per cent decrease in the variable cost of production. In the simple example shown in Figure 1, the market is in equilibrium at point A where the supply curve S₀ intersects the demand curve D₀, resulting in quantity Q₀ and price P₀. A new technology decreases the variable cost of production by the amount AC so the industry supply curve initially shifts from S₀ to S₁. As more producers adopt the technology and respond to the incentive of lower costs to expand output, a new equilibrium is reached at point B resulting in quantity Q₁and price P₁. These price and quantity changes allow changes in gross industry benefits (and benefits to particular market segments when more than one market level is modelled) to be estimated. These are calculated as changes in “producer surplus” and “consumer surplus”. Standard formulae are used to make these calculations (Mounter et al. 2007)^[1].

Figure 1: Market equilibrium with a cost-reducing technology

Successful promotion campaigns are modelled as vertical parallel shifts in the relevant demand curves in the market where the promotion is assumed to take place. A one per cent upward shift represents a one per cent increase in consumers’ willingness to pay as a result of the promotion. For example, in Figure 2, an effective advertising campaign raises consumer willingness-to-pay by AC, so the industry demand curve initially shifts from D₀ to D₁. As producers respond to the incentive of higher prices to expand output, a new equilibrium is reached at point B resulting in quantity Q₁ and price P₁. However in this case it is assumed that the advertising campaign is funded by a levy on producers, which raises the variable cost of production and shifts the industry supply curve from S₀ to S₁. The new market equilibrium is therefore at point D with quantity Q₂ and price P₂. Again, these price and quantity changes allow changes in “producer surplus” and “consumer surplus” to be calculated using standard formulae.

Figure 2: Market equilibrium with a generic advertising program and a levy

A simplified representation of the Australian sheep and wool industries structure is depicted Figure 3. In the EDM the industries are horizontally disaggregated into Merino sheep and non-Merino sheep. Merino sheep are further separated according to agricultural zone and production enterprise within each zone. Breeding intention splits Merino ewes in the high rainfall and wheat-sheep zones into Merino and non-Merino lamb producing enterprises. Merino sheep not used for breeding purposes are classified as dry sheep and are grouped together. As such, Merino wethers and Merino hoggets within each zone are combined as a single enterprise or sector. This regional disaggregation allows for the evaluation of individual investments specific to an agricultural zone or commodity type. This has particular relevance to evaluation of R&D investments where new technologies may not be applicable, nor adopted, Australia wide.

Australian wool production is divided into four main diameter categories corresponding to Australian Bureau of Statistics wool export categories of 19 micron (μm) and finer, 20-23 μm, 24-27 μm and 28 μm or broader. Wool of the same diameter classification within each zone is assumed homogeneous in quality. Vertical disaggregation of the wool industry includes the warehousing, export and domestic early-stage processing sectors. The warehouse sector is assumed to include wool handling, storage, testing and associated selling costs. The majority of Australian wool production is exported in its raw greasy form with the remainder subjected to some degree of early-stage processing before being exported as scoured wool, carbonised wool or wool tops. Limited quantities of wool tops are used as inputs in domestic later-stage processing such as spinning and weaving. Early-stage processing of wool in Australia is separated into scouring, carbonising and top making sectors. Post-sale costs such as transport, dumping and shipment preparation for greasy wool are included in the export sector.

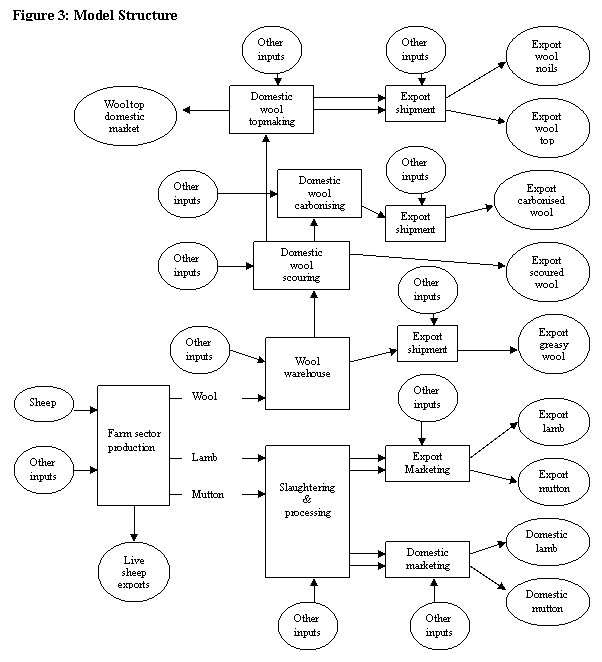
Vertical disaggregation of the sheepmeat supply chain beyond the farm gate consists of processing and marketing sectors. The processing sector undertakes all slaughtering and processing activities necessary to produce lamb and mutton for the export market and carcasses of lamb and mutton for sale to domestic retailers. The domestic marketing or retail sector processes the carcasses and packages the products for sale to final consumers. This sector comprises supermarkets, butchers and integrated abattoir or independent boning rooms that undertake the same process.

The resulting EDM of the Australian sheepmeat and wool industries is a system of 295 equations with 295 endogenous variables. The modelling approach involves linear approximation of changes in prices and quantities of inputs and outputs arising from new technology or promotion. In using this method the industries are represented by a system of demand and supply relationships with base prices and quantities used to define an initial equilibrium. The impact of any exogenous change to the system, such as a new technology or promotion campaign, is modelled as a shift in demand or supply from that initial equilibrium as shown in Figures 1 and 2.

As is typical in EDM analysis it is assumed that all production functions exhibit constant returns to scale and profit maximisation is an implicit behavioural assumption of each industry sector within the model. The impacts of new technologies in various industry sectors or successful promotion campaigns in various product markets are represented by 42 exogenous supply and 19 exogenous demand shift variables, respectively. Interested readers are referred to Mounter et al. (2007) for further detail on the model.

The explicit contributions of this model are two-fold. Firstly, the cross-commodity relationships of the industries are accounted for within the model. For example, wool and lamb are produced jointly while lamb and mutton are substitutes in domestic consumption. Published models to date have mostly been single industry approaches that largely ignore the multi-product nature of the Australian sheepmeat and wool industries (Mullen et al. 1989; Mullen and Alston 1994; Hill et al. 1996). Secondly, a high degree of industry disaggregation allows for the evaluation of individual investments specific to an agricultural zone or commodity type. Some new technologies may only be applicable in specific regions.

3. Data Requirements

Estimates of market parameters and base equilibrium price and quantity values for all industry sectors are required to solve the model. Typically, the base equilibrium values are specified as average prices and quantities over a number of years, to dampen the impact of seasonal effects or other anomalies or market disruptions present in a particular year. One such disruption that occurred in 2002 was that Australian woolgrowers began operating in a free market for the first time in almost thirty years after the last of the 4.7 million-bale wool stockpile was sold. In order for the data to reflect current market values and production systems, the base equilibrium values, and associated input cost and output revenue shares, used in the model were specified as the average prices and quantities for 2002-03 to 2004-05 inclusive. The market elasticities were specified according to relevant empirical studies, theoretical considerations and subjective judgement. The parameter values represent a medium-run time frame of approximately three years. In other words, it takes roughly three years for the industry to adjust to a new equilibrium after a shock to the initial market equilibrium. The surplus change estimates derived from the model can be interpreted as the average annual surplus changes after the industry has adjusted to the new equilibrium, assuming immediate and complete industry adoption of the new technology or promotion investment.^[4]

There are 61 possible R&D and promotion investment scenarios. Consequently, this study is limited to nine alternative hypothetical investment scenarios that cover some of the many product/market destination/market sector possibilities. These are listed in Table 1.

4. Results

The potential annual economic benefits and the distribution of these benefits among the various industry sectors for the nine hypothetical scenarios are summarised in Table 2a and Table 2b.

Total Benefits

In terms of absolute value (last row of the tables), wool production research (Scenario 6) and greasy wool promotion (Scenario 9) provide the largest potential total returns ($24.52 million and $22.11 million, respectively), based on the chosen prices, quantities and parameter values and the assumptions made about the impact and timing of R&D and promotion displacements. For the investment scenarios specifically related to lamb research or promotion, the largest potential total return is for domestic lamb promotion (Scenario 5, $14.61 million) followed by lamb production research (Scenario 1, $9.23 million).

Table 1: Selected hypothetical scenarios

Scenario 1: Lamb Production Research

A one per cent cost reduction in lamb production resulting from any farm technology that reduces the cost of producing lambs. The technology applies to all non-Merino and Merino lambs produced for slaughter in all three agricultural zones.

Scenario 2: Sheepmeat Processing Research

A one per cent cost reduction in the sheepmeat processing sector resulting from new technologies or improvements in management that reduces the cost of slaughtering and processing lamb and mutton.

Scenario 3: Domestic Lamb Marketing Research

A one per cent cost reduction in the domestic lamb marketing and retail sector resulting from new technologies or improvements in management.

Scenario 4: Export Lamb Promotion

A one per cent increase in the ‘willingness to pay’ by export lamb consumers due to promotion or changes in taste in the overseas market.

Scenario 5: Domestic Lamb Promotion

A one per cent increase in the ‘willingness to pay’ by domestic lamb consumers due to promotion or changes in taste in the domestic market.

Scenario 6: Wool Production Research

A one per cent cost reduction in wool production resulting from any farm technology that reduces the cost of producing wool. The technology applies to all types of wool grown in all three agricultural zones.

Scenario 7: Wool Warehouse and Brokerage Research

A one per cent cost reduction in the wool warehouse and brokerage sector resulting from new technologies or improvements in management that reduces wool storage, handling, testing or selling costs.

Scenario 8: Wool Scouring Research

A one per cent cost reduction in the domestic wool scouring sector resulting from new technologies or improvements in management.

Scenario 9: Greasy Wool Export Promotion

A one per cent increase in the ‘willingness to pay’ by export consumers of greasy wool due to promotion or changes in taste in the overseas market.

Distribution of Benefits

The exogenous shifts in investment in Scenarios 1, 3, 4 and 5 simulate either new technologies or promotions related specifically to lamb while Scenario 2 includes both lamb and mutton. With the exception of export promotion (Scenario 4), domestic consumers are the main beneficiaries in each scenario receiving between 30.8 and 48.7 per cent of the total benefits. In general, as overseas demand for Australian lamb is more elastic than domestic demand, and the share of production consumed domestically is greater than that exported, surplus gains for domestic consumers should be considerably larger than those received by overseas consumers. Nevertheless, shares of the total benefits collected by overseas consumers are significant (12.9 per cent to 30.6 per cent). Further, due to the joint nature of production, wool export quantities also increase as lamb production increases in all four domestic lamb investment scenarios.

Depending on the scenario in question, purchasers of Australian greasy and processed wool are the recipients of 60 per cent to 67 per cent of the additional surplus gained by all overseas consumers, as a result of R&D in the lamb industry.

Table 2a: Economic benefits ($ million) and distribution of total benefits (%) to various industry sectors: Scenarios 1-5

	Scenario 1	Scenario 2	Scenario 3	Scenario 4	Scenario 5
Sheep & Wool Producers	$m %	$m %	$m %	$m %	$m %
Non-Merino ewes	0.91 9.85	0.43 6.64	0.32 7.13	0.70 11.03	1.18 8.05
Merino ewes^a - high rainfall zone	0.30 3.28	0.15 2.38	0.11 2.49	0.24 3.87	0.41 2.81
Merino ewes^b- high rainfall zone	0.14 1.48	0.11 1.72	0.03 0.71	0.08 1.23	0.12 0.82
Merino ewes^a - wheat-sheep zone	0.66 7.16	0.30 4.68	0.25 5.46	0.53 8.39	0.90 6.15
Merino ewes^b- wheat-sheep zone	0.46 4.98	0.18 2.72	0.11 2.42	0.24 3.80	0.40 2.73
Merino ewes - pastoral zone	0.12 1.25	0.14 2.20	0.02 0.45	0.06 0.92	0.08 0.53
Merino wethers/hoggets - high rainfall zone	-0.15 -1.63	0.01 0.21	-0.04 -0.82	-0.07 -1.14	-0.13 -0.91
Merino wethers/hoggets - wheat-sheep zone	-0.20 -2.17	0.02 0.27	-0.05 -1.08	-0.09 -1.50	-0.17 -1.19
Merino wethers/hoggets - pastoral zone	-0.05 -0.49	0.09 1.39	-0.02 -0.37	-0.02 -0.35	-0.06 -0.39
Subtotal Producers	2.19 23.72	1.45 22.20	0.74 16.38	1.66 26.25	2.72 18.61
Wool Warehouse/Brokers	0.04 0.41	0.02 0.30	0.01 0.18	0.02 0.30	0.03 0.21
Wool Processors	0.05 0.55	0.03 0.44	0.01 0.23	0.02 0.38	0.04 0.26
Wool Exporters	0.05 0.51	0.02 0.38	0.01 0.23	0.02 0.37	0.04 0.26
Sheepmeat Processors	0.71 7.64	0.84 12.91	0.35 7.70	0.76 12.05	1.27 8.71
Sheepmeat Exporters	0.02 0.21	0.02 0.15	0.00 0.10	0.03 0.45	0.01 0.07
Domestic Sheepmeat Retailers	0.51 5.51	0.36 5.35	0.61 13.87	0.21 3.39	1.50 10.28
Overseas Consumers
Greasy wool	1.54 16.70	0.84 12.94	0.32 7.09	0.74 11.78	1.18 8.10
Processed wool	0.36 3.92	0.20 3.11	0.07 1.62	0.17 2.71	0.27 1.85
Lamb	0.90 9.70	0.61 9.34	0.17 3.79	1.44 22.77	0.63 4.28
Mutton	0.08 0.91	0.13 2.02	0.03 0.67	0.05 0.82	0.11 0.73
Live sheep	-0.06 -0.60	-0.04 -0.65	-0.01 -0.22	-0.03 -0.40	-0.04 -0.26
Subtotal Overseas Consumers	2.83 30.63	1.74 26.76	0.59 12.94	2.38 37.68	2.15 14.69
Domestic Consumers	2.85 30.82	2.04 31.27	2.20 48.68	1.21 19.09	6.89 47.16
Total Benefit	9.23 100	6.51 100	4.53 100	6.32 100	14.61 100

Table 2b: Economic benefits ($ million) and distribution of total benefits (%) to various industry sectors: Scenarios 6-9

	Scenario 6	Scenario 7	Scenario 8	Scenario 9
Sheep & Wool Producers	$m %	$m %	$m %	$m %
Non-Merino ewes	0.36 1.47	0.01 1.25	0.00 0.00	0.22 1.00
Merino ewes^a - high rainfall zone	0.36 1.48	0.01 0.93	0.00 0.98	0.27 1.23
Merino ewes^b- high rainfall zone	1.03 4.20	0.05 3.90	0.01 3.52	1.05 4.76
Merino ewes^a - wheat-sheep zone	0.57 2.31	0.02 1.53	0.01 1.69	0.40 1.82
Merino ewes^b- wheat-sheep zone	1.31 5.34	0.07 5.70	0.02 5.36	1.45 6.55
Merino ewes^b - pastoral zone	0.48 1.97	0.02 1.41	0.00 1.32	0.35 1.56
Merino wethers/hoggets - high rainfall zone	1.71 6.97	0.07 6.30	0.02 5.69	1.68 7.60
Merino wethers/hoggets - wheat-sheep zone	1.73 7.06	0.07 6.40	0.02 5.96	1.62 7.32
Merino wethers/hoggets - pastoral zone	0.10 0.40	0.02 1.32	0.00 1.22	0.32 1.45
Subtotal Producers	7.64 31.20	0.33 28.74	0.10 25.51	7.36 33.28
Wool Warehouse/Brokers	0.17 0.69	0.05 4.66	0.00 0.72	0.21 0.94
Wool Processors	0.29 1.17	0.02 1.36	0.07 16.51	-0.09 -0.43
Wool Exporters	0.21 0.87	0.01 1.03	0.00 1.12	0.25 1.11
Sheepmeat Processors	0.79 3.24	0.02 2.12	0.00 1.63	0.52 2.36
Sheepmeat Exporters	0.03 0.14	0.00 0.10	0.01 0.01	0.03 0.12
Domestic Sheepmeat Retailers	0.47 1.91	0.01 1.11	0.00 0.80	0.27 1.22
Overseas Consumers
Greasy wool	8.29 33.82	0.45 38.93	-0.04 -8.78	11.23 50.77
Processed wool	2.04 8.34	0.11 9.68	0.22 52.81	-0.67 -3.05
Lamb	0.74 3.03	0.02 1.63	0.01 1.10	0.39 1.76
Mutton	0.37 1.53	0.02 1.36	0.00 0.11	0.35 1.57
Live sheep	0.68 2.76	0.03 2.41	0.01 1.21	0.61 2.79
Subtotal Overseas Consumers	12.13 49.47	0.63 54.02	0.20 48.56	11.91 53.84
Domestic Consumers	2.78 11.34	0.08 6.86	0.02 5.06	1.67 7.56
Total Benefit	24.52 100	1.16 100	0.42 100	22.11 100

^a Ewes joined to produce non-Merino lambs ^b Ewes joined to produce Merino lambs

Promotion of lamb in Australia’s export markets and lamb production research (Scenarios 4 and 1, respectively) provide sheep and wool producers with the highest percentage share of total benefits from the five scenarios. In terms of benefit shares, sheep and wool producers fare much better from export lamb promotion than domestic lamb promotion. Relative to domestic demand, export demand is highly price elastic. Therefore, benefit gains to overseas consumers of Australian lamb from an increase in export demand will be small, allowing more of the benefits to flow back to producers, processors and marketers than is the case for an increase in the domestic demand for lamb. Australian consumers receive close to half of the total benefits from domestic promotion of lamb but only a one-fifth share from export lamb promotion. Conversely, overseas consumers gain a much larger share of the total benefits from export lamb promotion than from domestic lamb promotion.

Dry sheep enterprises experience negative surplus changes in response to four of the five lamb research and promotion investments, reinforcing the argument for inclusion of the multiple components of the sheep and wool industries in the analyses.

Sheepmeat processors obtain total benefit shares in the range of 7.6 per cent to 12.9 per cent in the five scenarios. Domestic retailers gain between 3.4 per cent and 13.9 per cent of returns. The wool warehouse/brokerage, domestic wool processing, wool export and sheepmeat export sectors gain small amounts, all receiving benefit shares of less than 1 per cent in each scenario. Elastic supplies of inputs and small value added to products in these sectors restrict the total benefit shares.^[5]

As the majority of Australian wool is exported in either greasy or semi-processed form, overseas consumers gain significant shares of the total returns in each of the four wool investment scenarios. Purchasers of greasy or semi-processed wool acquire upwards of 85 per cent of the total benefits going abroad with the remainder split among overseas consumers of lamb, mutton and live sheep. Domestic wool processors incur a loss of surplus from successful overseas promotion of Australian greasy wool.

Domestic consumers receive much smaller shares of the total benefits from wool-related investments (5.1 per cent to 11.3 per cent). Additional surplus gains are mostly the outcome of lower retail prices for lamb resulting from increased supply.

Sheep and wool producers gain the greatest share of total returns from greasy wool promotion (Scenario 9) and wool production research (Scenario 6). Unlike lamb-specific investments where some of the additional surplus gains accruing to lamb producing enterprises are transferred from the dry sheep enterprises, the wool-specific investment scenarios deliver gains to all sheep enterprises in the model. Other industry sectors individually receive up to 4 per cent of the total benefits.

General Comments about the Results

A number of qualifications need to be stated in relation to the results reported in Tables 2a and 2b. Firstly, they are gross potential benefits. They are derived from hypothetical one per cent exogenous shifts in the relevant sector demand or supply curves, and the costs involved in implementing the one per cent shifts are not taken into consideration. Therefore, as pointed out earlier by Zhao et al. (2001) and Mounter et al. (2005), comparison of the monetary returns from the different scenarios can only be made under the assumption that the investment costs required to implement the equal demand or supply curve shifts are the same in each sector. To demonstrate, if the monetary investments in lamb production research and sheepmeat processing research were identical (equal $ investment induces equal percentage shift), sheep and wool producers as a whole would prefer lamb production research ($2.19 million) to sheepmeat processing research ($1.45 million). For sheep and wool producers to be indifferent as to which sector the research funds are directed into, investment in sheepmeat processing would need to be approximately 51 per cent more efficient than investment in lamb production (2.19/1.45 = 1.51). In other words the size of the percentage shift necessary to generate the same returns to producers from sheepmeat processing research as from a 1 per cent cost reduction in lamb production would be 1.51 per cent. So, in terms of monetary gains, which investment scenario is preferred over another depends on the costs required to shift the demand or supply curves in the relevant market.

However, even without knowledge of the investment costs, the distributions of total benefits among industry sectors from alternative scenarios are directly comparable. The same amount of money invested in different industry sectors may result in demand or supply shifts of unequal size but the shares of total benefits among industry sectors for a particular scenario is independent of the magnitude of the initial shift (Zhao 1999, p.160). For example, the producers’ share of the total benefits from lamb production research (23.7 per cent in Scenario 1) is the same irrespective of the size of the percentage reduction in the cost of producing lamb. Recall though that the results are dependent on the assumptions made, and values chosen, for the various economic parameters and the price and quantity data used in the model.

Secondly, the annual flows of benefits are indicative of the returns assuming full adoption and complete market adjustment. In this study, a medium-run time frame is assumed for the industry to adjust to a new equilibrium after an exogenous shock. The estimated economic gains are the annual benefits generated after the new equilibrium has been obtained. Inevitably there will be lags between the commencement of an investment and the time taken to reach maximum adoption. Thus, the extent of annual benefit and cost flows will differ from year to year.

Thirdly, the hypothetical scenarios assume that R&D and promotion are effective in shifting the relevant supply and demand curves by one per cent. There is an extensive literature on the measurement of the effectiveness of R&D expenditures (Alston et al. 1995) and of promotion expenditures (Freebairn et al. 2005). Further, the alternative ways of funding the investment expenditures to bring about the supply and demand shifts are not examined.^[6]

5. Sensitivity Analysis

Pannell (1997) offers some thoughts on how and why modellers should take account of the uncertain nature of the input data they use in their models. Uncertainty can come about in EDMs through the underlying price and quantity data used to fix the points of initial equilibrium and in the underlying market parameter values that indicate how producers and consumers will respond to shocks to this equilibrium.

Prices and Quantities

Discrete sensitivity analysis (where one or more prices, quantities or parameters are given different discrete values) can be used to demonstrate the impacts that different price and quantity data may have on the results. To illustrate, Scenario 5 (domestic lamb promotion) was re-run with the retail prices of lamb and mutton reduced by 20 per cent. As expected with the total retail value of lamb reduced by 20 per cent, total surplus was also 20 per cent less. The benefits to all industry sectors were smaller with the gains to sheep and wool producers falling by $0.13 million from $2.72 million to $2.59 million. Conversely, the share of total benefits accruing to sheep and wool producers increased from 18.6 per cent to 22.2 per cent. Therefore, it is important to bear in mind that total benefits and their distributions may be influenced by assumptions regarding prices and quantities, highlighting the need for accurate and timely data and care in selecting “representative” years in the analysis.

Parameter Values

The share of total benefits received by each industry sector or group from research or promotion investments may also alter as a result of changes in the values of certain parameters. Discrete sensitivity analysis can provide some indication of how critical the selection of market parameter values may be to the distributions of benefit changes. However, discrete sensitivity analysis has some obvious limitations. When there are numerous uncertain parameters within the model it becomes impractical to try to examine the impact of all possible combinations of alternative parameter values. Even if empirical estimation for every combination of values were attainable, little inference can be made about which values represent the true parameter values and, hence, which combinations of values are most likely to yield the true benefit changes. Given that there are almost 50 separate parameter values in this model, a more rigorous method is used to account for any uncertainty in market parameters. The approach is based on stochastic sensitivity analysis presented by Zhao et al. (2000).

In using this approach, subjective probability distributions are specified for the parameters, with any necessary theoretical constraints or correlations imposed through the distributions. The probability distributions assigned to the parameters were either truncated normal distributions or mixed truncated normal and exponential distributions. Specifying a normal distribution implies there is equal probability that values will fall either side of the subjectively specified mode (most likely value), with approximately 68 per cent of the data within one standard deviation and 95 per cent within two standard deviations of the mode. In instances where the subjective view was that truncated normal distributions were not representative of the probabilities that the parameter values may assume, mixed truncated normal and exponential distributions were used to provide the necessary skewed shape. In some instances, parameter probability distributions are conditional on other subjectively specified parameter distributions. For example, where two different parameters are assumed to take the same mode, a mixed distribution may be chosen for the first parameter with the second parameter normally distributed around the first distribution.

Sign restrictions were placed on the parameters based on theoretical constraints. For example, export and domestic own-price elasticities of demand, and product transformation elasticities are expected to have negative signs. Truncating the distribution from above at zero restricts these parameters to take negative values. Own-price elasticities of supply, input substitution elasticities and cross-price domestic demand elasticities are expected to have positive signs. Truncating the distribution from below at zero restricts these values to take positive values. Placing sign restrictions on a parameter may cause the distribution to become asymmetric which has certain implications for the probabilities for particular ranges of values. However, for most parameters in the model, the truncation is more than three standard deviations from the mode and has little effect on the distributions.

The subjectively specified probability distributions and implied 95 per cent probability intervals (95% PI) for the parameters in the EDM are listed in the Appendix for interested readers ^[7].

The model was simulated 2000 times, each time selecting a different value for each of the parameter values from the specified probability distributions. This process resulted in 2000 sets of price and quantity changes and hence 2000 sets of economic benefit measures. Summary statistics for the benefit accruing to sheep and wool producers corresponding to each scenario are presented in Table 3a and Table 3b.^[8] The figures on the left side of each column are the benefits in millions of dollars and those on the right side are the percentage shares of the total benefits. The rows headed “base” refer to the results from the base version of the model as reported in Tables 2a and 2b. The other rows refer to summary measures across the 2000 simulations.

Given the probability distributions specified for each of the market elasticities, the values in Table 3a and Table 3b provide a measure of the variability of the benefit changes. For example, in Scenario 1 the mean benefit to sheep producers from lamb production research is $2.24 million with an average 24.2 per cent share of the total benefits. This compares to the point estimates from the base run (reproduced from Table 2a) of $2.19 million and 23.7 per cent of the total benefits.

Table 3a: Summary statistics: Benefit changes ($million) and benefit shares (%) to sheep and wool producers, scenarios 1-5

	Scenario 1 Lamb Production Research	Scenario 2 Sheepmeat Processing Research	Scenario 3 Lamb Retail Marketing Research	Scenario 4 Export Lamb Promotion	Scenario 5 Domestic Lamb Promotion
Sheep Producers	$m %	$m %	$m %	$m %	$m %
Base	2.19 23.72	1.45 22.20	0.74 16.33	1.66 25.46	2.72 18.61
Mean	2.24 24.24	1.32 20.28	0.66 14.57	1.65 25.31	2.67 18.34
Standard deviation	0.35 3.79	0.28 4.30	0.19 4.19	0.24 3.79	0.43 2.93
95% prob. interval	1.67 18.07 3.05 33.00	0.67 10.29 1.84 28.26	0.23 5.08 1.00 22.07	1.23 18.89 2.19 33.59	1.96 13.46 3.61 24.79

Table 3b: Summary statistics: Benefit changes ($million) and benefit shares (%)to sheep and wool producers, scenarios 6-9

	Scenario 6 Wool Production Research	Scenario 7 Wool Warehousing Research	Scenario 8 Wool Scouring Research	Scenario 9 Export Wool Promotion
Sheep Producers	$m %	$m %	$m %	$m %
Base	7.64 31.20	0.33 28.45	0.10 23.81	7.36 33.28
Mean	7.53 30.72	0.30 25.86	0.09 21.43	7.28 32.93
Standard deviation	0.83 3.38	0.07 3.80	0.02 4.76	0.87 3.93
95% prob. interval	6.02 24.55 9.30 37.93	0.09 7.76 0.41 35.34	0.02 4.76 0.13 30.95	5.59 25.28 9.02 40.80

The subjective 95 per cent PI is different from a conventional sampling theory confidence interval in that it is derived from subjective prior distributions (Zhao 1999). It is obtained by discarding the lowest 2.5 per cent and highest 2.5 per cent of the 2000 simulated benefit changes. The remaining first and last values form an estimate of the interval. Thus, for Scenario 1 we have 95 per cent confidence that sheep producers will receive between $1.67 million and $3.05 million, or between 18 per cent to 33 per cent of the total benefits, from this particular type of on-farm research. Comparing the subjective 95 per cent PI with approximately two standard deviations from the mean allows for any asymmetry in the distribution to be discovered. For example, two standard deviations from the mean in Scenario 1 provide interval estimates of $1.54 million to $2.94 million to sheep producers indicating the distribution is skewed slightly to the right. Non-symmetry of this type occurs because of the truncated normal, and mixed normal and exponential distributions specified for the market parameters.

Further analysis can be undertaken to draw some conclusions about the robustness of the results given the uncertainty of numerous parameters. Inspection of the summary statistics in Tables 3a and 3b reveals that as a consequence of the different range of values drawn for the different parameters in the simulations, the 95 per cent PI from some scenarios overlap in part with the 95 per cent PI in other scenarios. Thus, the possibility exists that the ordering of investment scenario preferences for an industry group or sector may alter for particular combinations of parameter values. For instance, in Scenario 1 and Scenario 5 (Table 3a), the 95 per cent PI for the percentage shares of total benefits accruing to sheep and wool producers overlap. This suggests that for some parameter value combinations, sheep and wool producers may prefer domestic promotion of lamb (Scenario 5) to on-farm research (Scenario 1), the opposite outcome from the base model percentage share results.

Probabilities can be calculated from the simulation data to determine the likelihood that one investment scenario may deliver a smaller or larger benefit share to a particular industry sector than another investment scenario. Based on the percentage shares of total benefits received in Tables 2a and 2b, the preferences by Australian sheep and wool producers’ for alternative investments are listed in Table 4.

Table 4: Investment scenario preferences of sheep and wool producers (base model)

Rank

Lamb-Specific Investment Scenarios

Rank

Wool-Specific Investment Scenarios

Export Promotion of Lamb (S4)

Lamb Production Research (S1)

Sheepmeat Processing Research (S2)

Domestic Promotion of Lamb (S5)

Domestic Lamb Marketing Research (S3)

Export Promotion of Greasy Wool (S9)

Wool Production Research (S6)

Wool Warehouse Research (S7)

Wool Scouring Research (S8)

Table 5 displays the probabilities, calculated from the simulation data, that the percentage share of total gains from one scenario exceeds another scenario.^[9] Consistent with the base model results, the calculated probabilities in Table 5 for the lamb-specific investment scenarios indicate that sheep and wool producers will always receive a larger share of the total benefits from lamb production research (Scenario 1) than domestic lamb marketing research (Scenario 3) or domestic lamb promotion (Scenario 5). The base run results also show the benefit share to sheep and wool producers in Scenario 1 is larger than the share of total gains from sheepmeat processing research (Scenario 2). However, the calculated probability (Table 5) suggests there is a 20 per cent chance that the reverse may be true. The result is likely to be influenced by the fact that lamb and mutton are both included in Scenario 2. As many of the procedures are identical, new technology that reduces the cost of slaughtering and processing lamb is also assumed to reduce the cost of slaughtering and processing mutton. Therefore, sheep and wool producers receive some of the benefits associated with a cost reduction in mutton processing in addition to those from a cost reduction in lamb processing.

Another important factor to consider in parameter choices is the relative sizes of related parameters. For example, Holloway (1989) showed that the relative sizes of retail demand elasticities and input substitution elasticities in downstream sectors could affect the returns to farmers. The subjective probability distributions specified for the input substitution elasticities between primary commodity inputs and other inputs in the Appendix allow for 95 per cent PI of 0.01 to 0.74, with 25 per cent of values greater than 0.2. Based on Holloway’s results, if the input substitution elasticity in the lamb marketing sector were larger than the input substitution elasticity in the sheepmeat processing sector, there could be a reduction in the returns to sheep and wool producers. Less robust results with similar size probabilities are also shown for sheep and wool producers’ preferences for sheepmeat processing research (Scenario 2) over domestic promotion of lamb (Scenario 5), domestic promotion of lamb (Scenario 5) over domestic lamb marketing research (Scenario 3) and export promotion of lamb (Scenario 4) over lamb production research (Scenario 1). In comparing the two lamb promotion scenarios, the base model results show that sheep and wool producers prefer export promotion of lamb (Scenario 4) to domestic promotion of lamb (Scenario 5). The simulation data confirm this is always the case.

With respect to the wool-specific scenarios, sheep and wool producers will almost certainly prefer promotion of greasy wool exports (Scenario 9) to wool production research (Scenario 6), warehouse and brokerage research (Scenario 7) and wool scouring research (Scenario 8). The calculated probabilities suggest that, at most, there is only a 4 per cent chance otherwise. The base model results indicate that sheep and wool producers favour wool production research (Scenario 6) over wool warehouse and brokerage research (Scenario 7) and wool scouring research (Scenario 8). The probabilities in Table 6 verify this, though for Scenario 7 the results are somewhat less robust. The least conclusive of all the wool investment comparisons is the preference by sheep and wool producers for research in the warehouse and brokerage sector (Scenario 7) over wool-scouring research (Scenario 8). As pointed out earlier, the extent of input substitution possibilities in these off-farm sectors may impact on the returns to sheep and wool producers. Given the size and multi-product nature of the EDM it is likely that the numerous product transformation possibilities within the model also play a role in determining the outcomes.

Table 5: Probabilities of differences in sheep and wool producers’ investment scenario preferences

Lamb-Specific Investment Scenarios

P (Lamb Production Research) > (Sheepmeat Processing Research) = 80%

P (Lamb Production Research) > (Domestic Lamb Marketing Research) = 100%

P (Lamb Production Research) > (Domestic Promotion of Lamb) = 100%

P (Sheepmeat Processing Research) > (Domestic Lamb Marketing Research) = 100%

P (Sheepmeat Processing Research) > (Domestic Promotion of Lamb) = 80%

P (Export Promotion of Lamb) > (Lamb Production Research) = 86%

P (Export Promotion of Lamb) > (Domestic Promotion of Lamb) = 100%

P (Domestic Promotion of Lamb) > (Domestic Lamb Marketing Research) = 80%

Wool-Specific Investment Scenarios

P (Wool Production Research) > (Wool Warehouse Research) = 89%

P (Wool Production Research) > (Wool Scouring Research) = 95%

P (Export Promotion of Greasy Wool) > (Wool Production Research) = 96%

P (Export Promotion of Greasy Wool) > (Wool Warehouse Research) = 99%

P (Export Promotion of Wool) > (Wool Scouring Research) = 96%

P (Wool Warehouse Research) > (Wool Scouring Research) = 83%

The sensitivity analysis has shown, even if some particular combinations of parameter values provide conclusions to the contrary, that overall, the preferences by sheep and wool producers for one particular investment scenario over another investment scenario, derived from the base model, are relatively robust. With the exception of sheepmeat processing research (Scenario 2), for reasons outlined above, the probabilities that sheep and wool producers prefer on-farm research to off-farm research range from 90 per cent to 100 per cent. Sheep and wool producers always favour research in lamb production and promotion of export lamb over promotion of lamb in the domestic market. At most, there is only a 4 per cent chance that sheep and wool producers would prefer other wool-specific investments to export promotion of greasy wool.

6. Implications and Conclusions

The EDM reported in this paper was developed to enable analysis of total benefit changes and their distribution among industry sectors from a range of possible exogenous changes impacting on the Australian sheep and wool industries. These include, but are not limited to, the evaluation of alternative broad types of research and promotion investments or the impacts of government market interventions. The model can also be used to evaluate specific R&D or promotion investments. The model provides a high degree of industry disaggregation not previously developed in other models, and specifically accounts for the extensive cross-commodity interactions present within the Australian sheep and wool industries.

The usefulness of the model was demonstrated by estimating the potential total industry returns and their distribution among various industry sectors and market participants for nine hypothetical R&D and promotion scenarios. The largest potential annual returns to the Australian sheep and wool industries, and to sheep and wool producers, were from effective R&D that reduces the cost of wool production by 1 per cent ($25.5 million) and from effective promotion of greasy wool in export markets that increases demand by 1 per cent ($22.1 million). These monetary gains are only comparable under the assumption of equal investment efficiency. However, the benefit shares do provide a meaningful comparison no matter what the actual level of benefits. For example, sheep and wool producers as a group receive the greatest share of total benefits from investment in greasy wool promotion (33.3 per cent) and wool production research (31.2 per cent), cost reduction in the domestic lamb marketing and retail sector generates the largest share of benefits to domestic consumers (48.7 per cent), while overseas consumers receive around 54 per cent of the additional gains from research in the wool warehouse sector research and from export promotion of greasy wool.

As with all these types of models, the results are conditional on the values specified for the parameters, and the prices and quantities used to define the initial equilibrium point. Unfortunately, in such a large model, data limitations meant that subjective judgement often had to be used to specify these values, as information on elasticities, and base prices and quantities were scarce or non-existent. This uncertainty raises the issue of the robustness of the results to alternative values. Consequently, a stochastic sensitivity analysis was undertaken to estimate summary statistics and establish 95 per cent probability intervals for the economic surplus changes.

Overall, the preferences of sheep and wool producers for one research or promotion investment scenario over another as suggested from the base model were found to be relatively robust to alternative parameter values. For example, the simulation results verified that sheep and wool producers always prefer export promotion of lamb to domestic promotion of lamb. Alternatively, the chance that sheep and wool producers would be in favour of off-farm research over on-farm research was calculated to be less than 10 per cent. Again, it should be stressed that these results are dependent on the assumption of equal investment efficiency. Similar types of implications for other investment alternatives can be drawn from the tabulated results.

From an industry perspective, the information provided by the model can assist priority-setting and policy decisions within the industry by helping to identify the total returns, and the beneficiaries of those returns, from alternative broad R&D or promotion investment areas. The model is not only of relevance to levy-paying producers, other industry groups and providers of R&D and promotion but also the community in general, as a component of the investment is funded by government and consumers share in the benefits from investment.

Finally, the EDM provides the structure to enable proper cost-benefit analyses to be undertaken on a project once information on investment costs and likely impacts are known. For example, the EDM described in this paper has been used in recent months to evaluate the potential economic returns from the QPLU$ genetic selection technology (Mounter et al. 2008).

7. References

Alston, J.M., Norton, G.W. and Pardy, P.G. (1995), Science Under Scarcity: Principles and Practice for Agricultural Research Evaluation and Priority Setting, Cornell University Press, Ithaca and London.

Australian Bureau of Agricultural and Resource Economics (ABARE) (2006), Australian Wool 06.1, ABARE, Canberra, March.

Australian Bureau of Agricultural and Resource Economics (ABARE) (2007a), Australian Lamb 07.1,ABARE, Canberra, April.

Australian Bureau of Agricultural and Resource Economics (ABARE) (2007b), Australian Commodity Statistics 2007, ABARE, Canberra, December.

Australian Wool Innovation (AWI) (2007), Company Funding, Sydney. http://www.wool.com.au/About_AWI/company_funding/page_2144.aspx

Freebairn, J.W., Goddard, E.W. and Griffith, G.R. (2005), “When can a generic advertising program increase farmer returns?”, Australasian Agribusiness Review Volume 13, Paper 20 (October 5). http://www.agrifood.info/review/2005/Freebairn_Goddard_Griffith.html

Hill, D.J., Piggott, R.R. and Griffith, G.R. (1996), “Profitability of incremental expenditure on fibre promotion”, Australian Journal of Agricultural Economics 40: 151-74.

Holloway, G.J. (1989), “Distribution of research gains in multistage production systems: further results”, American Journal of Agricultural Economics 71(2): 338-43.Meat and Livestock Australia (MLA) (2006), Australia’s Sheepmeat Industry – fast facts 2006, Meat and Livestock Australia, Sydney. http://www.mla.com.au

Mounter, S., Griffith, G.R. and Piggott, R.R. (2005), “The payoff from generic advertising by the Australian pig idustry, in the presence of trade”, Australasian Agribusiness Review, Volume 13, Paper 4 (February 22). http://www.agrifood.info/Publications_Review/Mounter_Griffith_Piggott.htm

Mounter, S., Griffith, G., Piggott, R., Fleming, E. and Zhao, X. (2007), An Equilibrium Displacement Model of the Australian Sheep and Wool Industries, Economic Research Report No. 38, NSW Department of Primary Industries, Armidale, December (under review).

Mounter, S.W., Griffith, G.R. and Mullen, J.D. (2008), “Selecting for fibre diameter and fleece weight: A market-level assessment of the QPLU$ Merino breeding project”, paper presented at the 52nd Annual Conference of the Australian Agricultural and Resource Economics Society, Rydges Lakeside, Canberra, 5 - 8 February.

Mullen, J.D. and Alston, J.M. (1994), “The impact on the Australian lamb industry of producing larger leaner lamb”, Review of Marketing and Agricultural Economics 62(1): 453-61.

Mullen, J.D., Alston, J.M. and Wohlgenant, M.K. (1989), “The impact of farm and processing research on the Australian wool industry”, Australian Journal of Agricultural Economics 33(1): 32-47.

Pannell, D.J. (1997), “Sensitivity analysis of normative economic models: Theoretical framework and practical strategies”, Agricultural Economics 16: 139-152.

Piggott, R.R. (1998), “Spending the pastoralist’s levy dollars: promotion vs research”, Inaugural Public Lecture, University of New England, 11 September, Armidale.

Zhao, X. (1999), The economic impacts of new technologies and promotions on the Australian beef industry, unpublished PhD thesis, University of New England, Armidale.

Zhao, X., Griffiths, W.E., Griffith, G.R. and Mullen, J.D. (2000), “Probability distributions for economic surplus changes: the case of technical change in the Australian wool industry”, Australian Journal of Agricultural and Research Economics 44(1): 83-106.

Zhao, X., Griffith, G.R. and Mullen, J.D. (2001), “Farmer returns from new technologies in the Australian beef industry: on-farm research versus off-farm research”, Australasian Agribusiness Review, Volume 9, Paper 1. http://www.agrifood.info/review/2001/Zhao.html

Appendix: Subjective probability distributions and 95% probability intervals for market parameters

Market Parameter

Sheep Supply Elasticities Non-Merino

Sheep High Rainfall Zone Sheep

Wheat-sheep Zone Sheep

Pastoral Zone Sheep

Probability Distribution

~ N(1.2, 0.25 2|>0)

~ N(1.0, 0.20 2|>0)

~ N(1.2, 0.25 2|>0)

~ N(0.8, 0.15 2|>0)

95% PI

(0.7, 1.7)

(0.6, 1.4)

(0.7, 1.7)

(0.5, 1.1)

Other Factor Supply Elasticities

Wool Scouring,Carbonising and Topmaking

Wool Export Shipment

Wool Warehouse

Sheepmeat Processing

Sheepmeat Marketing

Farm Enterprises

~ N(1.0, 0.25 2|≥0)

~ N(2.5, 0.50 2|≥0)

~ N(2.0, 0.50 2|≥0)

~ N(3.0, 0.50 2|≥0)

(0.5, 1.5)

(1.5, 3.5)

(1.0, 3.0)

(2.0, 4.0)

Demand Elasticities

≤ 19 micron greasy wool, ≤ 19 scoured wool

20-23 micron greasy wool, 20-23 micron scoured wool

24-27 micron greasy wool, 24-27 micron scoured wool

≥ 28 micron greasy wool, ≥ 28 micron scoured wool

Wool Top, Carbonised Wool and Noils

Export Lamb

Export Mutton

Export Live Sheep

Domestic Lamb

Domestic Mutton

Lamb-mutton cross-price: η (QLD, PMD)

Mutton-lamb cross-price: η (QMD, PLD)

~ N(-1.0, 0.25 2|<0)

~ N(-1.2, 0.30 2|<0)

~ N(-1.9, 0.30 2|<0)

~ N(-2.0, 0.30 2|<0)

~ N(-1.5, 0.50 2|<0)

~ N(-2.5, 0.50 2|<0)

~ N(-5.0, 1.50 2|<0)

~ N(-2.0, 0.65 2|<0)

~ N(-1.5, 0.25 2|<0)

~ N(-1.4, 0.25 2|<0)

~ N(0.13, 0.05 2|≥0)

≡ (λ LD/λ MD)η (QLD,PMD)

(-0.5, -1.5)

(-0.6, -1.8)

(-1.3, -2.5)

(-1.4, -2.6)

(-0.5, -2.5)

(-1.5, -3.5)

(-2.0, -8.0)

(-0.7, -3.3)

(-1.0, -2.0)

(-0.9, -1.9)

(0.03, 0.21)

(0.20, 1.31)

Input Substitution Elasticities

(A) Between sheep and other inputs (Farm Enterprises)

Between wool and other inputs (Warehouse Sector)

Between wool and other inputs (Export Sector)

Between wool and other inputs (Processing Sectors)

Between wool and wool (Processing Sectors)

Between lamb and other inputs (Processing Sector)

Between lamb and other inputs (Marketing Sector)

Between mutton and other inputs (Processing Sector)

Between mutton and other inputs (Marketing Sector)

(B) Between greasy wool (same zone and micron range)

Between lamb (same quality)

Between mutton (samequality)

Between greasy wool (different zone, same micron)

Between non-Merino and Merino lamb

Product Transformation Elasticities

Between ≤ 19 micron and 20-23 micron greasy wools

Between 20-23 micron and 24-27 micron greasy wools

Between 24-27 micron and ≥ 28 micron greasy wools

Between wool and lamb (Farm)

Between mutton and live sheep (Farm)

Between wool and wool (Warehouse Sector)

Between wool and wool (Processing Sector)

Between export and domestic lamb

Between export and domestic mutton

~ N(0.065, 0.10 2|≥0) 0.7 prob.

~ 0.08 + Exp (4.1) 0.3 prob.

~ N(σ (A) , 0.05 2|≥0)

~ N(5.0, 1.70 2|≥0) 0.5 prob.

~ 4.5 + Exp (0.2) 0.5 prob.

~ N(σ (B) , 0.50 2|≥0)

~ N(2.0, 0.65 2|≥0)

~ N(-0.5, 0.20 2|≤0)

~ N(-0.25, 0.10 2|≤0)

~ N(-0.20, 0.05 2|≤0)

~ N(-1.80, 0.40 2|≤0)

~ N(-2.0, 0.50 2|≤0)

~ N(-0.10, 0.05 2|≤0)

~ N(-0.50, 0.20 2|≤0)

~ N(-1.0, 0.30 2|≤0)

(0.02, 0.75)

(0.01, 0.74)

(2.4, 19.5)

(2.3, 19.6)

(0.7, 3.3)

(-0.1, -0.9)

(-0.05, -0.45)

(-0.1, -0.3)

(-1.0, -2.6)

(-1.0, -3.0)

(0.0, -0.2)

(-0.1, -0.9)

(-0.4, -1.6)

Footnotes

^[1] Producer surplus is a measure of economic benefit to producers as a group defined as the difference between willingness-to-accept a price for their product and the price actually received, summed across all producers. Consumer surplus is a measure of economic benefit to consumers as a group defined as the difference between willingness-to-pay a price for a product and the price actually paid, summed across all consumers.

^[2] The full specification of the model is described in Mounter et al. (2007).

^[3] As defined by ABARE, agricultural production within Australia comprises three agricultural zones, high rainfall, wheat-sheep and pastoral.

^[4] Based on the specified three-year price averages and the average annual quantities for 2002-03 to 2004-05.

^[5] With relatively elastic supply the changes in producer surplus are smaller than with inelastic supply as the changes in price are smaller.

^[6] The distribution of the returns from lump-sum funded investments and levy-based systems will differ. An example can be found in Mounter et al. (2005).

^[7] See Mounter et al. (2007) for a discussion on the choice of these probability distributions.

^[8] To conserve space the summary statistics for the other industry sectors are not included but are available from the authors on request.

^[9] Similar probabilities can be calculated for the other industry sectors.